Software Tools for Data Analysis
STA 9750
Michael Weylandt
Week 13 – Thursday 2026-05-07
Last Updated: 2026-01-14

STA 9750 Week 13

Today: Final Project Presentation + Enrichment: Functional Tools in R

• Communicating Results (quarto) ✅
• R Basics ✅
• Data Manipulation in R ✅
• Data Visualization in R ✅
• Getting Data into R✅
• Statistical Modeling in R ⬅️

Today

Today

• Course Administration
• Warm-Up Exercise
• New Material
  • Linear Models
  • Computational Inference
  • Predictive Models
• Wrap-Up
  • Life Tip of the Day

Course Administration

GTA

Charles Ramirez is our GTA

• Wednesday Office Hours moved to 5:15-7:15 for greater access
  • Give a bit of flexibility on the front end for CR to get off work
• Grading Meta-Review #03 after Peer Feedback

Mini-Project #04

MP#04 - TBD

Peer feedback due 2026-05-24

Topics covered:

• Data Import
  • HTTP Request Construction (Week 9)
  • Tabular HTML Scraping (Week 11)
• \(t\)-tests
• Putting Everything Together

Grading in Progress

I owe you:

• MP#03 Grades & Meta-Review
• Selected Regrades

Course Support

• Synchronous
  • MW Office Hours 2x / week: Tuesdays + Thursdays 5pm
  • GTA Office Hours: Wednesdays at 5:15-7:15pm
• Asynchronous: Piazza (\(<20\) minute average response time)

Course Project

End of Semester Course Project:

• In-Class Final Presentations
  • Last week of class or during finals week (optional)
• Individual Report
  • 2026-05-21
• Group Report
  • 2026-05-21
• Peer Evaluations
  • 2026-04-02, 2026-05-21

See detailed instructions for rubrics, expectations, etc.

Course Project

• Proposals ✅
• Check-In ✅
• Final Presentation
• Final Reports
  • Group
  • Individual

Final Presentation

Next week! Review the Rubric!

• Overarching Question
• Motivation and Context: Why are you doing this project?
• Prior Art: What have others done in this space? What gap are you filling?
• Data Used: What and why? “SWOT” it
• Specific Questions: What questions and how do they tie back?
• Results of Specific
• Implications for Overarching
• Next Steps / Future Work

Non-Technical Presentation - You’re a “consultant” asked by a client to investigate

Final Reports

Group and Individual Reports

• Submitted via GitHub and Brightspace
• Everyone submit a separate link to group report

Deadline on “final exam” day

No late work accepted (I have to submit grades in 3 days before family arrives!)

Project Peer Feedback

New peer feeback mechanism (feedback welcome!)

• You have 100 points to allocate to teammates

Can’t assign points to yourself

Additionally, 8 optional qualitative questions (Brightspace) for peer evaluation

Submit a copy for each teammate - I will anonymize to give advice

• Due on same day as reports

If you don’t submit, you won’t receive any points

Final Project Grading

Rubric is set high to give me flexibility to reward teams that take on big challenges

Hard rubric => Grades are curved generously

Multiple paths to success

If your project is “easy” on an element (data import in particular), that’s great! Don’t spend the effort over-complicating things. Effort is better spent elsewhere

Pre-Assignments

No more pre-assignments!

Thank you for these!

Course Feedback

Reflection on course:

• How far have you come?
• What have you learned?
• What was helpful? What was unhelpful?

My (anonymous) feedback survey

This is in addition to the Baruch central course assesments.

Course Feedback

Used to improve future course offerings. Previous changes:

• Added a second round of project feedback
  • Help students “scope” projects suitably
• More applied analytics than programming exercises in HW
  • Other programming resources already online;
  • Many students have prior experience (Python, SQL)
  • More interest in Analytics than Software Engineering
• Added GitHub and Portfolio Construction
  • Give students evidence of skills to share with employers
• Increased interactivity of course materials

Course Feedback

Plans for future improvement:

• Move to 3 MPs
  • More time to focus on final presentations
• Extra Credit for in-class engagement (?)
• Move final presentations into finals week (?)

Other thoughts welcome!

Review Exercise

Review Exercise

Analysis of the countries of the world

In this final review exercise, you will use a combination of the skills developed in this course to create a map of the countries of the world.

See Lab #13 for details.

Breakout Rooms

Breakout	Team
1	TBD

Statistical Models in R

Formula Notation

R was designed for statistical analysis (originally called S)

Major contributions

• data.frame / tidy structure
• Formula language (“Wilkinson-Rogers notation”)

Formula Notation

In R, a formula is a special object defined by a ~

Most common structure

y ~ x1 + x2

Predict variable y using x1 and x2

• Modern R uses formulas in many other contexts
• Various extensions provided by packages

Modeling Functions

Basic modeling function: lm (linear model)

lm(body_mass ~ flipper_len, data=penguins)

Call:
lm(formula = body_mass ~ flipper_len, data = penguins)

Coefficients:
(Intercept)  flipper_len  
   -5780.83        49.69  

Modeling Functions

Call:
lm(formula = body_mass ~ flipper_len, data = penguins)

Coefficients:
(Intercept)  flipper_len  
   -5780.83        49.69  

• Provide model (formula) and data (data.frame) instead of \(X, y\)
• By default automatically includes an intercept term

Modeling Functions

Call:
lm(formula = body_mass ~ flipper_len + species, data = penguins)

Coefficients:
     (Intercept)       flipper_len  speciesChinstrap     speciesGentoo  
        -4031.48             40.71           -206.51            266.81  

Automatically:

• Encodes categorical (factor) variables
  • ?C for details
• Removes extra / redundant columns

Modeling Functions

Call:
lm(formula = body_mass ~ flipper_len * bill_dep, data = penguins)

Coefficients:
         (Intercept)           flipper_len              bill_dep  
          -36097.064               196.074              1771.796  
flipper_len:bill_dep  
              -8.596  

• * creates both ‘main’ effects and interactions

Modeling Functions

Call:
lm(formula = body_mass ~ flipper_len * species, data = penguins)

Coefficients:
                 (Intercept)                   flipper_len  
                   -2535.837                        32.832  
            speciesChinstrap                 speciesGentoo  
                    -501.359                     -4251.444  
flipper_len:speciesChinstrap     flipper_len:speciesGentoo  
                       1.742                        21.791  

• * of continuous and categorical creates ANCOVA

Modeling Functions

Many extensions

library(mgcv)
gam(body_mass ~ s(flipper_len) + s(bill_dep, by=species), data=penguins)

Family: gaussian 
Link function: identity 

Formula:
body_mass ~ s(flipper_len) + s(bill_dep, by = species)

Estimated degrees of freedom:
1.56 1.96 1.00 4.39  total = 9.91 

GCV score: 106441.7     

Fits a mixed-effect non-linear regression

Accessors

Helper functions to access fitted models:

m <- lm(body_mass ~ flipper_len*bill_dep + species, data=penguins)
coef(m)

         (Intercept)          flipper_len             bill_dep 
       -4844.4526376           27.3153209          200.0652179 
    speciesChinstrap        speciesGentoo flipper_len:bill_dep 
        -131.5598847         1283.9149548           -0.0900381 

Accessors

summary(m)

Call:
lm(formula = body_mass ~ flipper_len * bill_dep + species, data = penguins)

Residuals:
    Min      1Q  Median      3Q     Max 
-900.40 -238.12  -40.12  228.86 1085.32 

Coefficients:
                       Estimate Std. Error t value Pr(>|t|)    
(Intercept)          -4.844e+03  5.298e+03  -0.914   0.3611    
flipper_len           2.732e+01  2.699e+01   1.012   0.3123    
bill_dep              2.001e+02  2.945e+02   0.679   0.4973    
speciesChinstrap     -1.316e+02  5.192e+01  -2.534   0.0117 *  
speciesGentoo         1.284e+03  1.572e+02   8.166 6.51e-15 ***
flipper_len:bill_dep -9.004e-02  1.495e+00  -0.060   0.9520    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 331.3 on 336 degrees of freedom
  (2 observations deleted due to missingness)
Multiple R-squared:  0.8319,    Adjusted R-squared:  0.8294 
F-statistic: 332.5 on 5 and 336 DF,  p-value: < 2.2e-16

Accessors

In-sample / training prediction:

predict(m)

       1        2        3        5        6        7        8        9 
3536.088 3425.933 3767.175 3953.280 4114.393 3370.697 4059.188 3734.055 
      10       11       12       13       14       15       16       17 
4041.210 3370.937 3253.055 3359.674 4249.574 4409.196 3473.547 3949.683 
      18       19       20       21       22       23       24       25 
4310.849 3557.933 4380.573 3282.907 3510.456 3832.665 3528.570 3234.669 
      26       27       28       29       30       31       32       33 
3726.523 3568.992 3543.295 3286.946 3547.228 3091.116 3348.770 3550.685 
      34       35       36       37       38       39       40       41 
3649.683 3584.667 4358.365 4004.618 3473.685 3646.349 3686.382 3433.145 
      42       43       44       45       46       47       48       49 
3840.178 3627.582 4102.980 3308.480 3785.068 3616.823 3521.615 3620.406 
      50       51       52       53       54       55       56       57 
4249.574 3480.928 3752.137 3620.406 4168.735 3579.941 3774.117 3444.264 
      58       59       60       61       62       63       64       65 
3861.936 3150.175 3942.338 3308.480 4332.949 3326.821 3726.647 3319.386 
      66       67       68       69       70       71       72       73 
3690.091 3438.661 3788.765 3382.561 4099.392 3821.660 3711.885 3646.936 
      74       75       76       77       78       79       80       81 
3982.659 3547.223 3858.429 3444.955 3741.432 3213.485 3967.934 3466.569 
      82       83       84       85       86       87       88       89 
3719.903 3708.201 3971.549 3627.823 4161.456 3913.139 3722.836 3832.665 
      90       91       92       93       94       95       96       97 
3785.068 3947.038 4042.282 3345.161 3554.255 3433.358 4264.409 3748.477 
      98       99      100      101      102      103      104      105 
3884.079 2980.693 3781.480 3671.813 4336.307 3091.663 4004.618 3825.399 
     106      107      108      109      110      111      112      113 
3649.683 3724.236 4004.618 3223.682 4000.892 3570.903 4084.993 3660.980 
     114      115      116      117      118      119      120      121 
4092.056 4158.140 3847.595 3404.175 4325.323 3429.959 3722.836 3415.036 
     122      123      124      125      126      127      128      129 
4172.287 3094.759 4037.976 3150.955 4052.101 3591.249 3821.927 3499.815 
     130      131      132      133      134      135      136      137 
4152.595 3620.406 4037.358 3807.130 3961.028 3488.327 3547.223 3572.963 
     138      139      140      141      142      143      144      145 
4277.969 3235.117 3697.517 3551.367 3415.036 3129.468 3455.744 3470.758 
     146      147      148      149      150      151      152      153 
3638.615 3748.477 3557.933 3730.674 3734.055 3396.713 4012.327 4593.082 
     154      155      156      157      158      159      160      161 
5645.496 4729.996 5136.843 4932.508 4621.302 4846.576 5180.825 4577.078 
     162      163      164      165      166      167      168      169 
5095.145 4761.861 5247.505 4761.861 4898.577 4820.575 5201.160 4621.302 
     170      171      172      173      174      175      176      177 
5214.684 4776.450 5222.623 4974.450 4932.508 4880.489 5167.427 4679.518 
     178      179      180      181      182      183      184      185 
5040.932 4922.395 5022.862 4766.228 5206.763 5258.638 4722.075 4724.430 
     186      187      188      189      190      191      192      193 
5771.046 5116.634 5387.019 4735.779 5541.519 4587.236 4968.045 4605.370 
     194      195      196      197      198      199      200      201 
5462.316 4657.534 5048.826 5366.684 4876.212 4693.765 5444.335 4663.424 
     202      203      204      205      206      207      208      209 
5167.427 4748.112 4990.454 4784.344 5282.509 4966.475 5224.788 4641.637 
     210      211      212      213      214      215      216      217 
5152.685 4750.440 5310.513 4623.504 5160.634 4798.020 5563.784 4982.443 
     218      219      220      221      222      223      224      225 
5735.175 4888.419 5601.704 5008.480 5230.580 5048.826 5286.750 5286.750 
     226      227      228      229      230      231      232      233 
5038.686 5048.826 5591.689 4722.075 5387.019 4806.013 5482.561 4854.479 
     234      235      236      237      238      239      240      241 
5286.750 4872.577 5418.451 4727.795 5773.337 4992.494 4956.406 4763.990 
     242      243      244      245      246      247      248      249 
5771.046 5100.756 5737.430 4854.479 5454.431 4942.658 5434.276 5193.320 
     250      251      252      253      254      255      256      257 
5132.584 4602.212 5552.219 5126.721 5719.477 5113.215 5360.403 4832.086 
     258      259      260      261      262      263      264      265 
5221.639 4838.691 5270.998 4659.771 4885.198 5084.950 5547.870 5007.110 
     266      267      268      269      270      271      273      274 
5645.496 4912.317 5591.689 5201.160 5420.707 4761.861 4896.367 5330.669 
     275      276      277      278      279      280      281      282 
4908.772 5169.908 3540.254 3934.937 3803.451 3583.949 4015.194 3676.252 
     283      284      285      286      287      288      289      290 
3235.614 3723.470 3799.872 4058.951 3547.688 4029.896 3250.283 3807.980 
     291      292      293      294      295      296      297      298 
3342.480 4080.931 4051.660 3239.137 3616.917 3672.117 3147.253 3441.403 
     299      300      301      302      303      304      305      306 
3173.539 3839.989 3617.364 3869.332 3836.911 3946.146 3496.263 4255.776 
     307      308      309      310      311      312      313      314 
3173.539 4299.292 3191.862 3986.602 3745.120 3519.817 3690.368 4510.159 
     315      316      317      318      319      320      321      322 
3302.642 4237.616 4292.771 3338.444 3861.969 3478.892 3643.068 3880.767 
     323      324      325      326      327      328      329      330 
3488.846 4361.987 3558.318 3585.133 3446.958 3971.751 3456.344 4150.211 
     331      332      333      334      335      336      337      338 
3301.799 3832.867 3276.822 4186.569 3960.980 3865.558 4190.532 3206.875 
     339      340      341      342      343      344 
3453.107 4270.520 3833.665 3620.764 4202.192 3840.266 

Accessors

Out-of-sample / test prediction:

toppenguins <- penguins |> slice_max(body_mass, n=10)
predict(m, newdata=toppenguins)

       1        2        3        4        5        6        7        8 
5214.684 5771.046 5387.019 5420.707 5482.561 5547.870 4898.577 5201.160 
       9       10       11 
5591.689 5601.704 5591.689 

Accessors

For just lm:

methods(class="lm")

 [1] add1           alias          anova          case.names     coerce        
 [6] confint        cooks.distance deviance       dfbeta         dfbetas       
[11] drop1          dummy.coef     effects        extractAIC     family        
[16] formula        fortify        hatvalues      influence      initialize    
[21] kappa          labels         logLik         model.frame    model.matrix  
[26] nobs           plot           predict        print          proj          
[31] qqnorm         qr             residuals      rstandard      rstudent      
[36] show           simulate       slotsFromS3    summary        variable.names
[41] vcov          
see '?methods' for accessing help and source code

Even more for other models

Tidy tools - broom

The broom package provides tidyverse tools for working with models:

• tidy: gives information about model components (coefficients)
• glimpse: gives information about the model as a whole
• augment: applies the model to observations

Note: broom is not core tidyverse and needs to be loaded explicitly

broom

Fit a linear model:

Call:
lm(formula = mpg ~ wt + hp, data = mtcars)

Coefficients:
(Intercept)           wt           hp  
   37.22727     -3.87783     -0.03177  

Predict miles per gallon of 1973 cars using weight and horsepower

broom::glance

glance - model summary info

# A tibble: 1 × 12
  r.squared adj.r.squared sigma statistic  p.value    df logLik   AIC   BIC
      <dbl>         <dbl> <dbl>     <dbl>    <dbl> <dbl>  <dbl> <dbl> <dbl>
1     0.827         0.815  2.59      69.2 9.11e-12     2  -74.3  157.  163.
# ℹ 3 more variables: deviance <dbl>, df.residual <int>, nobs <int>

Don’t confuse with glimpse (summarize a data frame)

broom::tidy

tidy - model component info

# A tibble: 3 × 5
  term        estimate std.error statistic  p.value
  <chr>          <dbl>     <dbl>     <dbl>    <dbl>
1 (Intercept)  37.2      1.60        23.3  2.57e-20
2 wt           -3.88     0.633       -6.13 1.12e- 6
3 hp           -0.0318   0.00903     -3.52 1.45e- 3

Get more with conf.int=TRUE

# A tibble: 3 × 7
  term        estimate std.error statistic  p.value conf.low conf.high
  <chr>          <dbl>     <dbl>     <dbl>    <dbl>    <dbl>     <dbl>
1 (Intercept)  37.2      1.60        23.3  2.57e-20  34.0      40.5   
2 wt           -3.88     0.633       -6.13 1.12e- 6  -5.17     -2.58  
3 hp           -0.0318   0.00903     -3.52 1.45e- 3  -0.0502   -0.0133

broom::tidy

tidy returns a data.frame and works with tidyverse tools:

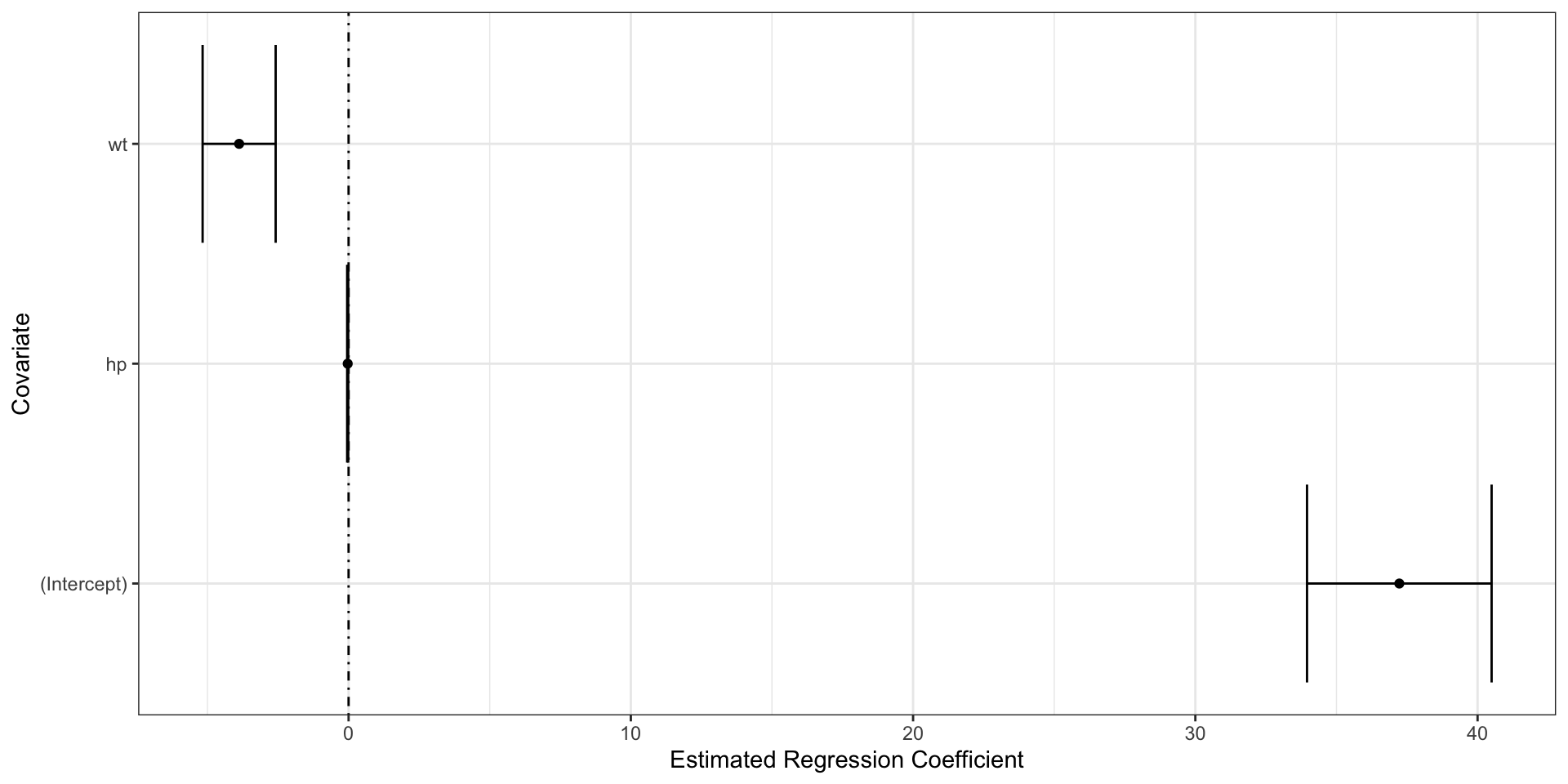
broom::augment

augment - apply the model (to training data by default)

# A tibble: 32 × 10
   .rownames     mpg    wt    hp .fitted .resid   .hat .sigma .cooksd .std.resid
   <chr>       <dbl> <dbl> <dbl>   <dbl>  <dbl>  <dbl>  <dbl>   <dbl>      <dbl>
 1 Mazda RX4    21    2.62   110    23.6 -2.57  0.0443   2.59 1.59e-2    -1.01  
 2 Mazda RX4 …  21    2.88   110    22.6 -1.58  0.0405   2.62 5.46e-3    -0.623 
 3 Datsun 710   22.8  2.32    93    25.3 -2.48  0.0602   2.59 2.07e-2    -0.985 
 4 Hornet 4 D…  21.4  3.22   110    21.3  0.135 0.0475   2.64 4.72e-5     0.0533
 5 Hornet Spo…  18.7  3.44   175    18.3  0.373 0.0369   2.64 2.74e-4     0.146 
 6 Valiant      18.1  3.46   105    20.5 -2.37  0.0672   2.60 2.16e-2    -0.948 
 7 Duster 360   14.3  3.57   245    15.6 -1.30  0.117    2.63 1.26e-2    -0.533 
 8 Merc 240D    24.4  3.19    62    22.9  1.51  0.116    2.62 1.68e-2     0.620 
 9 Merc 230     22.8  3.15    95    22.0  0.806 0.0600   2.63 2.19e-3     0.321 
10 Merc 280     19.2  3.44   123    20.0 -0.779 0.0469   2.63 1.55e-3    -0.308 
# ℹ 22 more rows

broom::augment

augment - pass newdata argument for out of sample evaluation

# A tibble: 1 × 5
    mpg    wt    hp .fitted .resid
  <dbl> <dbl> <dbl>   <dbl>  <dbl>
1    35  2.96   169    20.4   14.6

Modern Toyota is 14.6mpg better than expected in 1974

broom::augment

augment - pass newdata argument without \(y\) for pure prediction

# A tibble: 1 × 3
     wt    hp .fitted
  <dbl> <dbl>   <dbl>
1  2.94   200    19.5

Actual mpg is closer to 34!

broom

broom can be used with most models and tests:

    Pearson's product-moment correlation

data:  mpg and disp
t = -8.7472, df = 30, p-value = 9.38e-10
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
 -0.9233594 -0.7081376
sample estimates:
       cor 
-0.8475514 

broom

broom can be used with most models and tests:

# A tibble: 1 × 8
  estimate statistic  p.value parameter conf.low conf.high method    alternative
     <dbl>     <dbl>    <dbl>     <int>    <dbl>     <dbl> <chr>     <chr>      
1   -0.848     -8.75 9.38e-10        30   -0.923    -0.708 Pearson'… two.sided  

broom

Easily extends to groupwise analysis using nest/unnest and map:

# A tibble: 2 × 6
# Groups:   am [2]
     am     n estimate conf.low conf.high   p.value
  <dbl> <int>    <dbl>    <dbl>     <dbl>     <dbl>
1     1    13   -0.835   -0.949    -0.526 0.000383 
2     0    19   -0.793   -0.917    -0.529 0.0000519

So the correlation is larger for automatic transmissions (am=1), but we have more samples and a slightly smaller \(p\)-value for manual transmissions.

Exercise

Return to Lab #13 and practice manipulating the output of lm and the broom functions.

Computational Inference

Statistical Inference

Recall the basic theory of statistical tests - “goodness of fit”

• Select a baseline model (‘null hypothesis’)
• Select a quantity of interest (‘test statistic’)
• Determine distribution of test statistic under null hypothesis
• If observed test statistic is extreme (vis-a-vis null distribution of test statistic):
  • -> “doesn’t fit” and reject null

Statistical Theory

75+ Years of Theory

• Pick a null + test statistic
  • Compute “null distribution”

\(Z\)-values, \(t\)-values, \(p\)-values, etc.

Typically requires ‘big math’

Alternative:

• Let a computer do the hard work

Monte Carlo Simulation

Using a computer’s pseudo-random number generator (PRNG)

Repeat:

• Generate \(X_1, X_2, X_3, \dots\)
• Compute \(f(X_1), f(X_2), f(X_3), \dots\)

Sample average (LLN)

\[\frac{1}{n} \sum_{i=1}^n f(X_i) \to \mathbb{E}[f(X)]\]

Holds for arbitrary related quantities (quantiles, medians, variances)

Monte Carlo Simulation

Example: suppose we have \(X_i \buildrel{\text{iid}}\over\sim \mathcal{N}(0, \sigma^2)\) and we want to test \(H_0: \sigma=1\)

n <- 20
X <- rnorm(n, mean=0, sd=1.25)

sd(X)

[1] 0.8313391

How to test?

The Math Way

Per Cochran’s theorem, \(S \sim \sqrt{\frac{\chi^2_{n-1}}{n-1}} = \frac{1}{\sqrt{n-1}} \chi_{n-1}\) has a \(\chi\) (not \(\chi^2\)) distribution

library(chi)
critical_value <- qchi(0.95, df=n-1) / sqrt(n-1)
critical_value

[1] 1.259564

So reject \(H_0\) if \(S\) above critical value (1.26)

The Computer Way

To get a critical value

# A tibble: 1 × 1
  `quantile(test_statistic_null, 0.95)`
                                  <dbl>
1                                  1.23

The Computer Way

To get a \(p\)-value:

# A tibble: 1 × 1
  p_val
  <dbl>
1 0.854

Exercise

Return to Lab #13 and implement these ideas to test a rather strange null hypothesis.

infer

The infer package automates much of this for common tests

Many examples

Predictive Modeling in tidymodels

Agenda

• Predictive Modeling with tidymodels

Adapted from Case Study

tidymodels

Strength of R:

• Thousands of authors contributing packages to CRAN

Weakness of R:

• Thousands of authors contributing slightly incompatible packages to CRAN

No two modeling packages have exactly the same API. Makes changing between interfaces cumbersome

tidymodels

tidymodels attemps to provide a uniform interface to a wide variety of predictive Machine Learning tools

Advantages:

• Easy to swap out different algorithms to find the best

Disadvantages:

• Harder to take advantage of the strengths of each approach

I have dedicated my academic life to the differences in these methods, but 99% of the time, “black-box” prediction is good enough. In STA 9890/9891, we get into the weeds - not here.

ML vs Statistical Pipelines

Statistics / Data Science:

• Find the model that fits the data best
• Model should capture all important data features
• Interpretability
• History: Grounded in lab sciences where experiments are expensive and data is limited

ML vs Statistical Pipelines

Machine Learning:

• Find the model that predicts the data best
• No “perfect” model - just the best one we’ve found so far
• Black-box techniques are great, if effective
• History: Silicon Valley “at scale”

Validation based on of-of-sample or test predictions

Validating Predictive Power

How to check whether a model predicts well?

Need more data! But where to get more data?

• Actually get more data (hard, expensive, slow)
• Split data into parts - test/training split
• Cross-Validation
• Resampling

Today, we’ll primarily use a combination: Test/Train split & Cross-Validation!

Cross-Validation

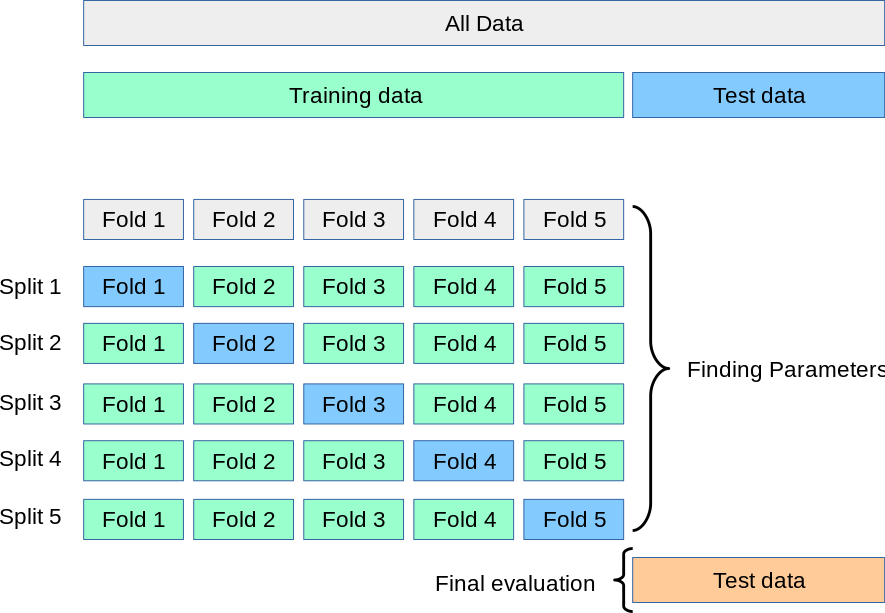
Cross-Validation is done on the estimator, not the fitted algorithm

tidymodels

tidymodels workflow:

• Initial Split
• Pre-Process
• Fit (many) models
• Select best
• Refit
• Test Set Assessment

tidymodels is very punny, so a bit hard to tell which step is which…

Acquire Data

library(tidymodels); library(readr)

hotels <- 
  read_csv("https://tidymodels.org/start/case-study/hotels.csv") |>
  mutate(across(where(is.character), as.factor))

glimpse(hotels)

Rows: 50,000
Columns: 23
$ hotel                          <fct> City_Hotel, City_Hotel, Resort_Hotel, R…
$ lead_time                      <dbl> 217, 2, 95, 143, 136, 67, 47, 56, 80, 6…
$ stays_in_weekend_nights        <dbl> 1, 0, 2, 2, 1, 2, 0, 0, 0, 2, 1, 0, 1, …
$ stays_in_week_nights           <dbl> 3, 1, 5, 6, 4, 2, 2, 3, 4, 2, 2, 1, 2, …
$ adults                         <dbl> 2, 2, 2, 2, 2, 2, 2, 0, 2, 2, 2, 1, 2, …
$ children                       <fct> none, none, none, none, none, none, chi…
$ meal                           <fct> BB, BB, BB, HB, HB, SC, BB, BB, BB, BB,…
$ country                        <fct> DEU, PRT, GBR, ROU, PRT, GBR, ESP, ESP,…
$ market_segment                 <fct> Offline_TA/TO, Direct, Online_TA, Onlin…
$ distribution_channel           <fct> TA/TO, Direct, TA/TO, TA/TO, Direct, TA…
$ is_repeated_guest              <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, …
$ previous_cancellations         <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, …
$ previous_bookings_not_canceled <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, …
$ reserved_room_type             <fct> A, D, A, A, F, A, C, B, D, A, A, D, A, …
$ assigned_room_type             <fct> A, K, A, A, F, A, C, A, D, A, D, D, A, …
$ booking_changes                <dbl> 0, 0, 2, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, …
$ deposit_type                   <fct> No_Deposit, No_Deposit, No_Deposit, No_…
$ days_in_waiting_list           <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, …
$ customer_type                  <fct> Transient-Party, Transient, Transient, …
$ average_daily_rate             <dbl> 80.75, 170.00, 8.00, 81.00, 157.60, 49.…
$ required_car_parking_spaces    <fct> none, none, none, none, none, none, non…
$ total_of_special_requests      <dbl> 1, 3, 2, 1, 4, 1, 1, 1, 1, 1, 0, 1, 0, …
$ arrival_date                   <date> 2016-09-01, 2017-08-25, 2016-11-19, 20…

Initial Split

# Stratified sampling to ensure balance
splits      <- initial_split(hotels, 
                             strata = children)

hotel_train <- training(splits)
hotel_test  <- testing(splits)

hotel_train

# A tibble: 37,500 × 23
   hotel   lead_time stays_in_weekend_nig…¹ stays_in_week_nights adults children
   <fct>       <dbl>                  <dbl>                <dbl>  <dbl> <fct>   
 1 City_H…         2                      0                    1      2 none    
 2 Resort…        95                      2                    5      2 none    
 3 City_H…        67                      2                    2      2 none    
 4 Resort…        47                      0                    2      2 children
 5 City_H…         6                      2                    2      2 children
 6 City_H…       130                      1                    2      2 none    
 7 City_H…        27                      0                    1      1 none    
 8 Resort…        16                      1                    2      2 none    
 9 Resort…        46                      0                    2      2 none    
10 City_H…       297                      1                    1      2 none    
# ℹ 37,490 more rows
# ℹ abbreviated name: ¹​stays_in_weekend_nights
# ℹ 17 more variables: meal <fct>, country <fct>, market_segment <fct>,
#   distribution_channel <fct>, is_repeated_guest <dbl>,
#   previous_cancellations <dbl>, previous_bookings_not_canceled <dbl>,
#   reserved_room_type <fct>, assigned_room_type <fct>, booking_changes <dbl>,
#   deposit_type <fct>, days_in_waiting_list <dbl>, customer_type <fct>, …

Pre-Process

A recipe is a set of steps used to ‘pre-process’ the data:

holidays <- c("AllSouls", "AshWednesday", "ChristmasEve", "Easter", 
              "ChristmasDay", "GoodFriday", "NewYearsDay", "PalmSunday")

lr_recipe <- 
  recipe(children ~ ., data = hotels) |> 
  step_date(arrival_date) |> 
  step_holiday(arrival_date, holidays = holidays) |> 
  step_rm(arrival_date) |> 
  step_dummy(all_nominal_predictors()) |> 
  step_zv(all_predictors()) |> 
  step_normalize(all_predictors())

lr_recipe

── Recipe ──────────────────────────────────────────────────────────────────────

── Inputs 

Number of variables by role

outcome:    1
predictor: 22

── Operations 

• Date features from: arrival_date

• Holiday features from: arrival_date

• Variables removed: arrival_date

• Dummy variables from: all_nominal_predictors()

• Zero variance filter on: all_predictors()

• Centering and scaling for: all_predictors()

Pre-Process

Declare response (children) and predictors (. = everything else)

lr_recipe <- 
  recipe(children ~ ., data = hotels) |> 
  step_date(arrival_date) |> 
  step_holiday(arrival_date, holidays = holidays) |> 
  step_rm(arrival_date) |> 
  step_dummy(all_nominal_predictors()) |> 
  step_zv(all_predictors()) |> 
  step_normalize(all_predictors())

Pre-Process

Use arrival_date to identify holiday arrivals:

lr_recipe <- 
  recipe(children ~ ., data = hotels) |> 
  step_date(arrival_date) |> 
  step_holiday(arrival_date, holidays = holidays) |> 
  step_rm(arrival_date) |> 
  step_dummy(all_nominal_predictors()) |> 
  step_zv(all_predictors()) |> 
  step_normalize(all_predictors())

Pre-Process

Convert categorical variables to numeric encoding:

lr_recipe <- 
  recipe(children ~ ., data = hotels) |> 
  step_date(arrival_date) |> 
  step_holiday(arrival_date, holidays = holidays) |> 
  step_rm(arrival_date) |> 
  step_dummy(all_nominal_predictors()) |> 
  step_zv(all_predictors()) |> 
  step_normalize(all_predictors())

Pre-Process

Drop variables that don’t vary:

lr_recipe <- 
  recipe(children ~ ., data = hotels) |> 
  step_date(arrival_date) |> 
  step_holiday(arrival_date, holidays = holidays) |> 
  step_rm(arrival_date) |> 
  step_dummy(all_nominal_predictors()) |> 
  step_zv(all_predictors()) |> 
  step_normalize(all_predictors())

Pre-Process

Standardize (mean 0, standard deviation 1) everything:

lr_recipe <- 
  recipe(children ~ ., data = hotels) |> 
  step_date(arrival_date) |> 
  step_holiday(arrival_date, holidays = holidays) |> 
  step_rm(arrival_date) |> 
  step_dummy(all_nominal_predictors()) |> 
  step_zv(all_predictors()) |> 
  step_normalize(all_predictors())

Fit Models

lr_model <- 
  logistic_reg(penalty = tune(), mixture = 1) |> 
  set_engine("glmnet")

lr_model

Logistic Regression Model Specification (classification)

Main Arguments:
  penalty = tune()
  mixture = 1

Computational engine: glmnet 

Select Best

Find a grid of parameters

lr_reg_grid <- data.frame(penalty = 10^seq(-4, -1, length.out = 30))

Perform CV splits:

lr_folds <- vfold_cv(hotel_train, v = 5)

Select Best

Define a workflow:

lr_workflow <-  
  workflow() |> 
  add_model(lr_model) |> 
  add_recipe(lr_recipe)

Fit workflow to a grid of parameters:

lr_results <- 
  lr_workflow |> 
  tune_grid(grid = lr_reg_grid,
            control = control_grid(save_pred = TRUE, 
                                   save_workflow=TRUE),
            resamples = lr_folds,
            metrics = metric_set(roc_auc))

Select Best

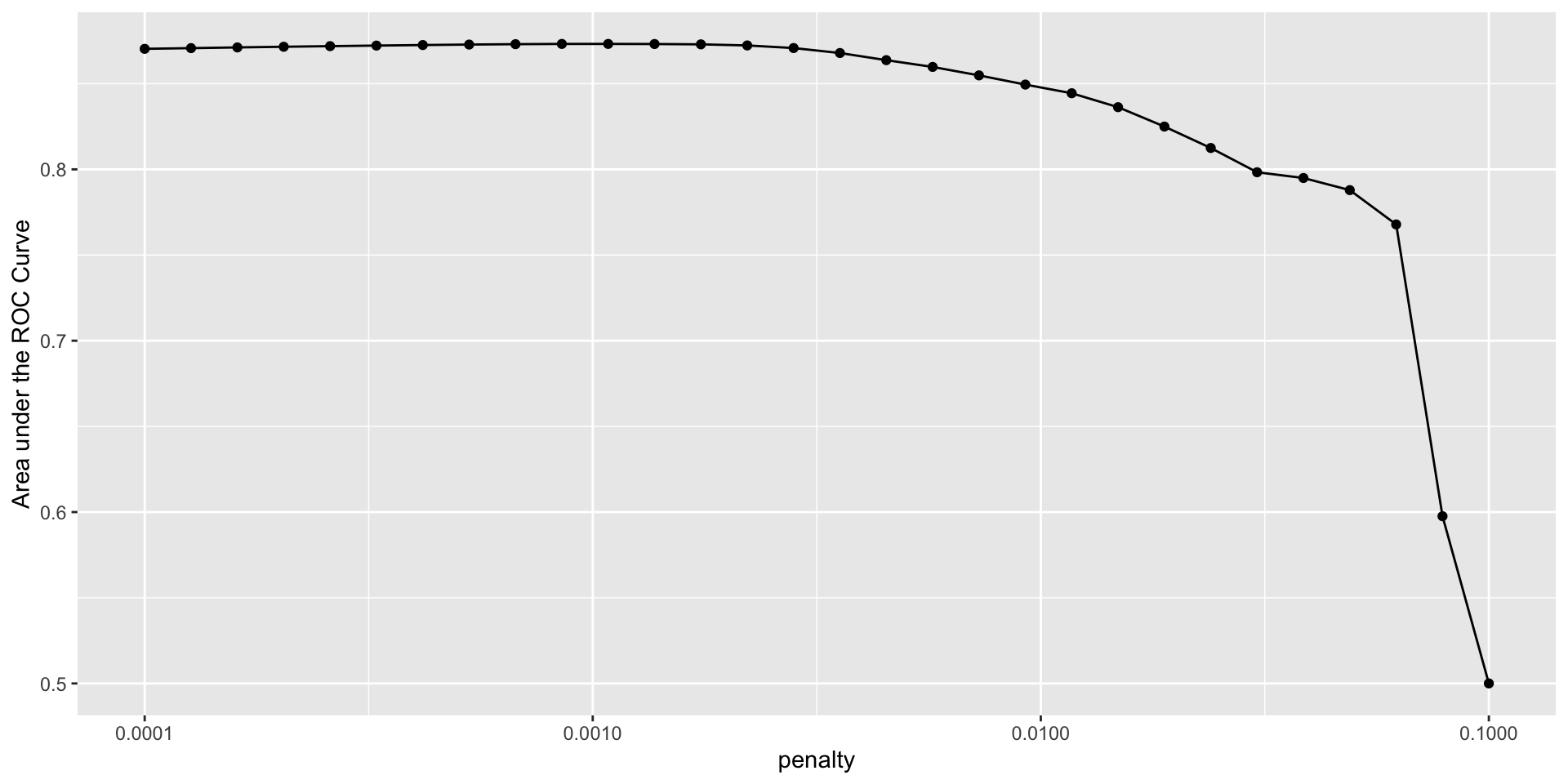
Visual examination

lr_results |> 
  collect_metrics() |> 
  ggplot(aes(x = penalty, y = mean)) + 
  geom_point() + 
  geom_line() + 
  ylab("Area under the ROC Curve") +
  scale_x_log10(labels = scales::label_number())

Select Best

lr_results |> show_best()

# A tibble: 5 × 7
   penalty .metric .estimator  mean     n std_err .config         
     <dbl> <chr>   <chr>      <dbl> <int>   <dbl> <chr>           
1 0.00108  roc_auc binary     0.873     5 0.00383 pre0_mod11_post0
2 0.000853 roc_auc binary     0.873     5 0.00396 pre0_mod10_post0
3 0.00137  roc_auc binary     0.873     5 0.00367 pre0_mod12_post0
4 0.000672 roc_auc binary     0.873     5 0.00407 pre0_mod09_post0
5 0.00174  roc_auc binary     0.873     5 0.00345 pre0_mod13_post0

lr_best <- lr_results |> select_best()
lr_best

# A tibble: 1 × 2
  penalty .config         
    <dbl> <chr>           
1 0.00108 pre0_mod11_post0

Refit Best Model

lr_best_fit <- lr_results |> fit_best()
lr_best_fit

══ Workflow [trained] ══════════════════════════════════════════════════════════
Preprocessor: Recipe
Model: logistic_reg()

── Preprocessor ────────────────────────────────────────────────────────────────
6 Recipe Steps

• step_date()
• step_holiday()
• step_rm()
• step_dummy()
• step_zv()
• step_normalize()

── Model ───────────────────────────────────────────────────────────────────────

Call:  glmnet::glmnet(x = maybe_matrix(x), y = y, family = "binomial",      alpha = ~1) 

    Df  %Dev   Lambda
1    0  0.00 0.078660
2    1  2.41 0.071670
3    2  5.08 0.065310
4    3  7.68 0.059500
5    4 10.13 0.054220
6    4 12.40 0.049400
7    4 14.09 0.045010
8    5 15.65 0.041010
9    5 17.04 0.037370
10   5 18.12 0.034050
11   5 18.98 0.031030
12   6 19.96 0.028270
13   6 20.82 0.025760
14   6 21.53 0.023470
15   7 22.16 0.021380
16   7 22.92 0.019480
17   8 23.51 0.017750
18   9 24.12 0.016180
19  10 24.71 0.014740
20  11 25.23 0.013430
21  11 25.65 0.012240
22  11 26.01 0.011150
23  12 26.32 0.010160
24  14 26.64 0.009257
25  16 26.93 0.008435
26  18 27.25 0.007685
27  21 27.65 0.007003
28  22 28.04 0.006380
29  26 28.51 0.005814
30  27 28.95 0.005297
31  31 29.37 0.004827
32  34 29.74 0.004398
33  36 30.13 0.004007
34  42 30.53 0.003651
35  46 30.92 0.003327
36  48 31.28 0.003031
37  49 31.58 0.002762
38  52 31.84 0.002517
39  55 32.08 0.002293
40  63 32.30 0.002089
41  66 32.51 0.001904
42  70 32.70 0.001735
43  75 32.86 0.001580
44  80 33.00 0.001440
45  85 33.13 0.001312
46  88 33.24 0.001196

...
and 46 more lines.

Test Set Assessment

predict(lr_best_fit, hotel_test)

# A tibble: 12,500 × 1
   .pred_class
   <fct>      
 1 none       
 2 none       
 3 children   
 4 none       
 5 none       
 6 none       
 7 none       
 8 none       
 9 none       
10 none       
# ℹ 12,490 more rows

Test Set Assessment

augment(lr_best_fit, hotel_test)

# A tibble: 12,500 × 26
   .pred_class .pred_children .pred_none hotel  lead_time stays_in_weekend_nig…¹
   <fct>                <dbl>      <dbl> <fct>      <dbl>                  <dbl>
 1 none                0.0103      0.990 City_…       217                      1
 2 none                0.0230      0.977 Resor…       143                      2
 3 children            0.771       0.229 Resor…       136                      1
 4 none                0.447       0.553 City_…        56                      0
 5 none                0.0486      0.951 City_…        80                      0
 6 none                0.0554      0.945 City_…       423                      1
 7 none                0.0208      0.979 Resor…       209                      2
 8 none                0.0216      0.978 City_…       134                      0
 9 none                0.0943      0.906 City_…        39                      0
10 none                0.112       0.888 Resor…        48                      1
# ℹ 12,490 more rows
# ℹ abbreviated name: ¹​stays_in_weekend_nights
# ℹ 20 more variables: stays_in_week_nights <dbl>, adults <dbl>,
#   children <fct>, meal <fct>, country <fct>, market_segment <fct>,
#   distribution_channel <fct>, is_repeated_guest <dbl>,
#   previous_cancellations <dbl>, previous_bookings_not_canceled <dbl>,
#   reserved_room_type <fct>, assigned_room_type <fct>, …

Test Set Assessment

my_metrics <- metric_set(accuracy, precision, recall, ppv, npv, sens, mcc)
augment(lr_best_fit, hotel_test) |>
    my_metrics(truth=children, estimate=.pred_class)

# A tibble: 7 × 3
  .metric   .estimator .estimate
  <chr>     <chr>          <dbl>
1 accuracy  binary         0.936
2 precision binary         0.705
3 recall    binary         0.345
4 ppv       binary         0.705
5 npv       binary         0.946
6 sens      binary         0.345
7 mcc       binary         0.465

Exercise

Return to Lab #13 and work through the remainder of the hotel stay case study

You’ll need to work through the data import elements as well

Other tidymodels tools

• Model Stacking
• Probabilistic Predictions
• Uncertainty Bounds (Conformal Inference)
• Multilevel (Mixed-Effect) Models
• Fairness Audits

More Reading

https://www.tidymodels.org/start/

Wrap Up

Wrap Up

Statistical Models in R:

• Classical models (lm)
• Computational Inference
• Predictive Models (tidymodels)

Upcoming Work

Upcoming work from course calendar

• Mini-Project #04 due on 2026-05-15 at 11:59pm ET
• Mini-Project #04 peer feedback due 2026-05-24
• End of Semester Project Submissions

Almost there!

Musical Treat