Attaching package: 'MASS'The following object is masked from 'package:dplyr':
selectdtree <- rpart(medv ~ . , data=Boston)
rpart.plot(dtree)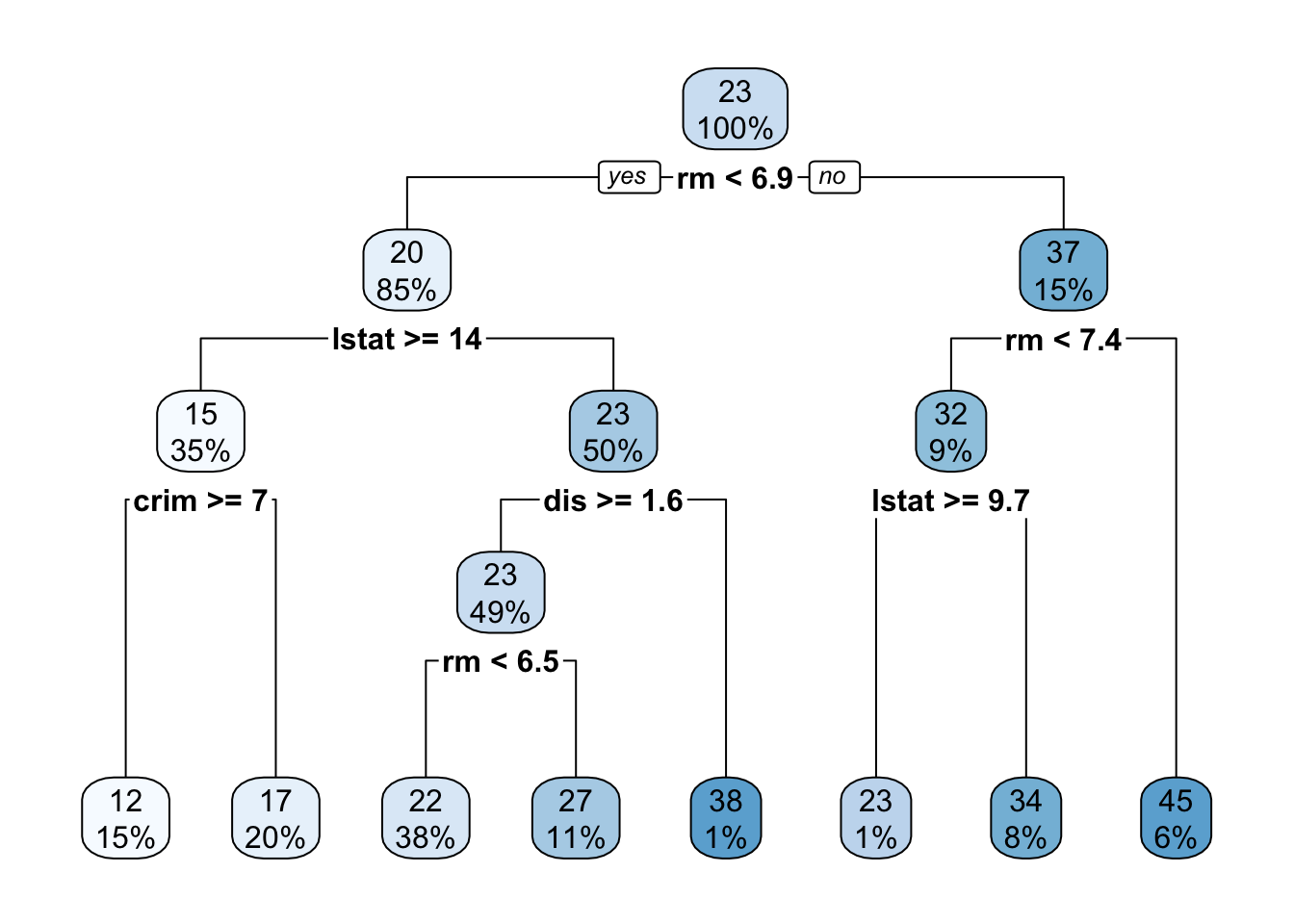
Michael Weylandt
January 13, 2026
\[\newcommand{\bx}{\mathbf{x}} \newcommand{\bb}{\mathbf{b}}\newcommand{\by}{\mathbf{y}}\]
Last week we discussed the ensemble learning technique known as bagging. Bagging, a contraction of ‘boostrap aggregation’ can be used to create an ensemble by training \(B\) copies of a given base learner on \(B\) distinct bootstrap samples, i.e., ‘faux’ data sets of \(n\) points obtained by sampling the original training data \(n\) times with replacement. Because these \(B\) trained base learners are essentially interchangeable, it is conventional to create the bagged prediction by a straight average (or majority vote if classification) of the individual base learners, though you will occasionally see the bagging base leraners combined in a ‘stacked’ fashion.
We showed that the MSE associated with a bagged ensemble of size \(B\) is:
\[\text{MSE}_{\text{Bagging}} = \text{Bias}^2_{\text{Base Learner}} +\underbrace{\rho\sigma^2 + \frac{1}{B}(1-\rho)\sigma^2}_{\text{Variance}} + \text{Irreducible Error}\]
and noted that, by sending \(B \to 0\), we reduce the ‘bootstrapping variance’ to 0 but that some ‘inherent variance’ remains from the training data.1 As we noted last week, this implies that our search for the optimal base learner should do three things:
If we can find something that does all of these, we will have a (near) optimal predictor (\(\text{MSE} \approx \text{Irreducible Error}\)). This is our primary goal for the day.
Before we move to our long-promised final base learner, let’s consider another advantage of bagging. We know that it is important to have ‘new’ data when assessing model performance. To date, we have obtained this ‘new’ data through variants of the hold-out principle, such as the test-train split or cross-validation: if it is important to have new data, it is important enough to set aside some of our putative training data for model assessment.
But bagging gives us another source of ‘unseen’ data: if we sample \(n\) points from a population of size \(n\) with replacement, approximately \(n/e \approx 2n/3\) points will be sampled, leaving \(n(1-e^{-1}) \approx n/3\) points unseen by each base learner. If these points were the same across each base learner, we would have a readily available test set. But then our whole bagging strategy would be essentially useless…
We can estimate the so-called ‘out-of-bag’ error (OOB) associated with each training point by computing the predictive performance on the ensemble of learners that haven’t seen that point. That is, instead of testing the performance of the whole ensemble, we take a ‘subensemble’ of the base learners that never saw that point. Repeating this process over all \(n\) training points (and creating \(n\) different sub-ensembles) we obtain an estimate of the OOB error. Clearly, OOB is not test error of the entire ensemble, but it is a useful quantity nevertheless.
Formally, we obtain the bagged ensemble and associated OOB error as follows:
For each training point, we expect it to occur in approximately \(B/e\) bootstrap samples and hence we have approximately \(1 - B/e \approx B/3\) base learners used for computing the OOB error. This isn’t quite as good as the full \(B\) samples we would use for a true test point, but since variance decreases quadratically in \(B\), this isn’t really a major loss.2
Ok - now it’s time to consider the final base learner of this course: decision trees. You are almost certainly already familiar with decision trees through diagrams like this:
Attaching package: 'MASS'The following object is masked from 'package:dplyr':
selectdtree <- rpart(medv ~ . , data=Boston)
rpart.plot(dtree)
Here, the tree is evaluated by applying a series of univariate binary decision rules ‘downwards’: that is, at each step, we ask one step about one variable and take the left or right branch as appropriate. The final terminus (or ‘leaf’) of the tree is then our prediction.
Decision trees are incredibly popular because they are easy to apply ‘mentally’ and suggest natural interpretations. Variables which are used to split early or split often are more important. Interestingly, decision trees also can be used to give an ‘intermediate prediction’ which is what we would get by stopping the prediction at that point. Splits which materially change the intermediate prediction are also more important.
But how should we actually fit a decision tree to data? This is, like bagging and computing OOB error, the sort of thing which is easy to understand intuitively, but comes with a significant amount of bookkeeping in practice.
Essentially, trees are fit by repeatedly asking the question: “What split would most reduce the error if my predictions stop here?” So, for the first split, the tree looks at each variable to determine its optimal split point, and then finds the optimal variable to split on. To find the optimal split point, we need to sort the data on that variable and then compute the ‘before’ and ‘after’ variance for each value. After finding the first split, the two ‘second level’ splits repeat this process on only the data in their path. That is, the two ‘second level’ splits are found on different data. The four ‘third level’ splits are found on four different data sets, etc.
Because the later splits are computed on different data sets, they almost always select different variables at each level (as in our example above, where the two ‘level two’ splits use the lstat and rm variables). Predictions are made by taking the average (or majority) of data left in that split.
Note that the splits need not be and typically are not ‘even’ splits along a variable. E.g., if we were doing a split on a variable that looks like
| Variable | Value |
|---|---|
| 1.0 | 1.0 |
| 1.1 | 0.9 |
| 1.2 | 1.1 |
| 1.3 | 1.4 |
| 100 | 500 |
| 105 | 550 |
The optimal split is clearly something like \(\texttt{Variable} < 1.3\) with conditional predictions of \(1.1\) and \(525\) in each split and split sizes of \(4\) and \(2\).
Clearly, if the tree is allowed to run ‘to completion’, there will be one data point left in each leaf and the tree can obtain 0 training error. That is, maximal decision trees are a very high complexity (low bias, high variance) model. On the other extreme, a ‘single split’ tree (often called a ‘stump’) will be low complexity (high bias, low variance). So we can take tree depth (number of levels) as a good proxy for model complexity. Like \(K\)-Nearest Neighbors, we can pick depth (complexity) by a suitable cross-validation or train-test scheme, but will soon see a better way.
Some other notes on trees:
CART (Classification and Regression Trees) or rpart (Recursive Partitioning) but most folks will know the term “decision trees” so I just use that.NA as very high or very low or use an explicit is.na decision ruleThere are tons of tiny little decisions in building trees, so I don’t recommend writing your own implementation. See, e.g., ?rpart.control for the fitting parameters used by the rpart package: other software will have similar options.
We are now ready to introduce the concept of random forests, which are almost bagged decision trees.
AdaBoostLogitBoostxgboostThere is randomness in our selection / acquisition of training data and nothing we do can completely remove it. Three cheers for large and well-constructed training sets, the unsung heros of machine learning!↩︎
Taking a typical choice of \(B = 500\), the OOB ensemble of (expected) \(316\) base learners will have a variance that is approximately \(500/316 \approx 1.6\) times higher than the ‘true’ ensemble. If \(B\) is large enough \((1-\rho)\sigma^2/B \approx 0\), \((1-\rho)\sigma^2/(B(1-e^{-1})) \approx 1.6(1-\rho)\sigma^2/B\) will also be negligible. Put another way, the bulk of the error in bagged ensembles comes from i) bias; ii) training data variance; and iii) irreducible error. The ‘not enough bootstraps’ contribution is typically quite small.↩︎