STA 9890 - Unsupervised Learning I: Dimension Reduction

Author

Michael Weylandt

\[\newcommand{\R}{\mathbb{R}}\newcommand{\bx}{\mathbf{x}}\newcommand{\by}{\mathbf{y}} \newcommand{\bv}{\mathbf{v}} \newcommand{\argmin}{\text{arg min}} \newcommand{\argmax}{\text{arg max}}\newcommand{\bX}{\mathbf{X}}\newcommand{\bI}{\mathbf{I}} \newcommand{\bR}{\mathbf{R}} \newcommand{\bzero}{\mathbf{0}}\]

Today, we begin our study of dimension reduction, the task of finding a simplified representation of your data. Before we begin formalizing DR, it is worthwhile to take a second to think about why we may want to perform DR as this will help us design suitable loss functions.

For now, let’s take DR ‘literally’ and assume that we’re trying to find a lower-dimensional representation: that is, given data points \(\bx_i \in \R^P\), we want to find \(\bx_i \in \R^p\) for some \(p \ll P\).1 Typically, \(P\) may be \(\mathcal{O}(1000-10000)\) and \(p\) will be \(\mathcal{O}(1-10)\). To identify the goals of DR, let’s think about the problems associated with large \(P\):

Clearly, in each of these, we’re going to have an easier time if we only have \(p\) features. And we could get \(p\) features quite easily by simply ‘throwing away’ most of our variables… But this has a rather obvious problem: if we throw away features willy-nilly, we might throw away the important ‘signal’ components of our data. So we want to build a model for automatically mapping from \(\R^P\) to \(\R^p\) that keeps the ‘signal’ (as best as we can estimate it).

Of course, this requires us to make the concept of ‘signal’ mathematically precise. We might consider goals like the following:

Mathematically, it will suffice to maintain inner products, as inner products generate distances and angles: that is, we want

\[\langle \bx, \by \rangle_{\R^P} \approx \langle f(\bx), f(\by) \rangle_{\R^p}\]

If you prefer a more statistical (as opposed to geometric) motivation, you can think of our desiderata as maintaining variances (distances) and correlations (angles) among aspects of our data: clearly, it suffices to maintain covariances (inner products).

PCA: First Steps

So, with that goal in mind, let’s start building our first dimension reduction technique. Consistent with our treatment of unsupervised learning, we’ll begin by assuming \(f\) is a linear operation and living in the world of MSE. As we build our method, let’s start by taking \(p=1\) (reducing down to a single dimension) but we’ll relax this in a bit.

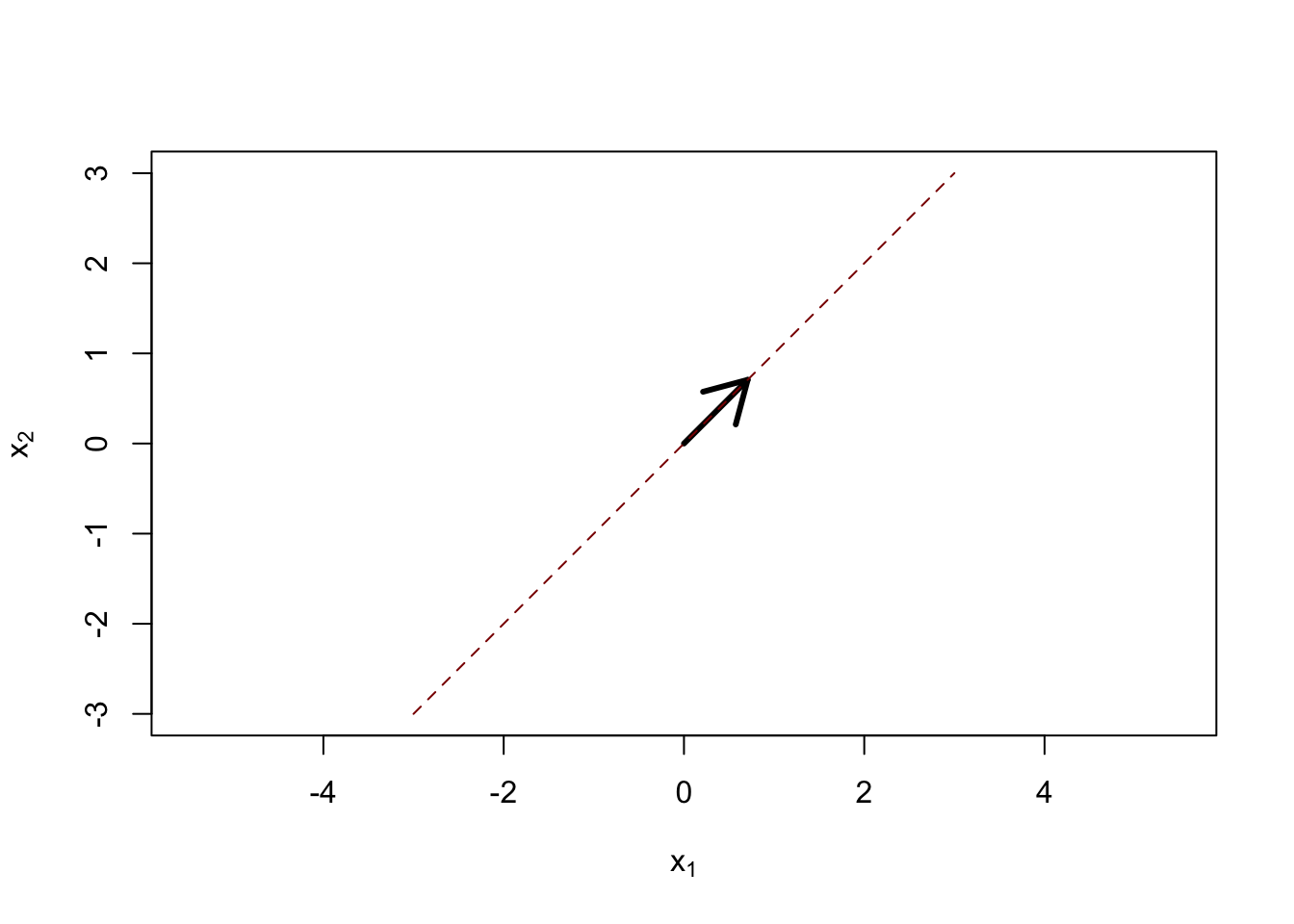
Our reduced dimension space can be parameterized by a single vector \(\bv \in \R^P\), with the reduced space being defined by \[\textsf{Span}(\bv) = \{\lambda \bv: \lambda \in \R\}.\] That is, our reduced space is the line generated by \(\bv\):

Here the black arrow is \(\bv\) and the dashed red line is \(\textsf{Span}(\bv)\). For a given space, the choice of \(\bv\) is clearly not unique: if we streteched or even flipped \(\bv\), \(\textsf{Span}(\bv)\) would remain unchanged, so we might as well assume \(\|\bv\|=1\) without loss of generality.

Once we have \(\bv\), how can we actually build the mapping \(f(\cdot): \R^P \to \textsf{Span}(\bv)\)? Well, if our goal is to minimize MSE, it makes sense to find the point in \(\textsf{Span}(\bv)\) that lies closest to our original point. It’s hopefully not too hard to convince yourself that this point is given by the projection of \(\bx\) onto \(\textsf{Span}(\bv)\), which is given by

\[\bv \frac{\langle \bx, \bv \rangle}{\langle \bv, \bv\rangle} = \langle \bx, \bv\rangle \bv = \bx^{\top}\bv \bv\]

Visually:

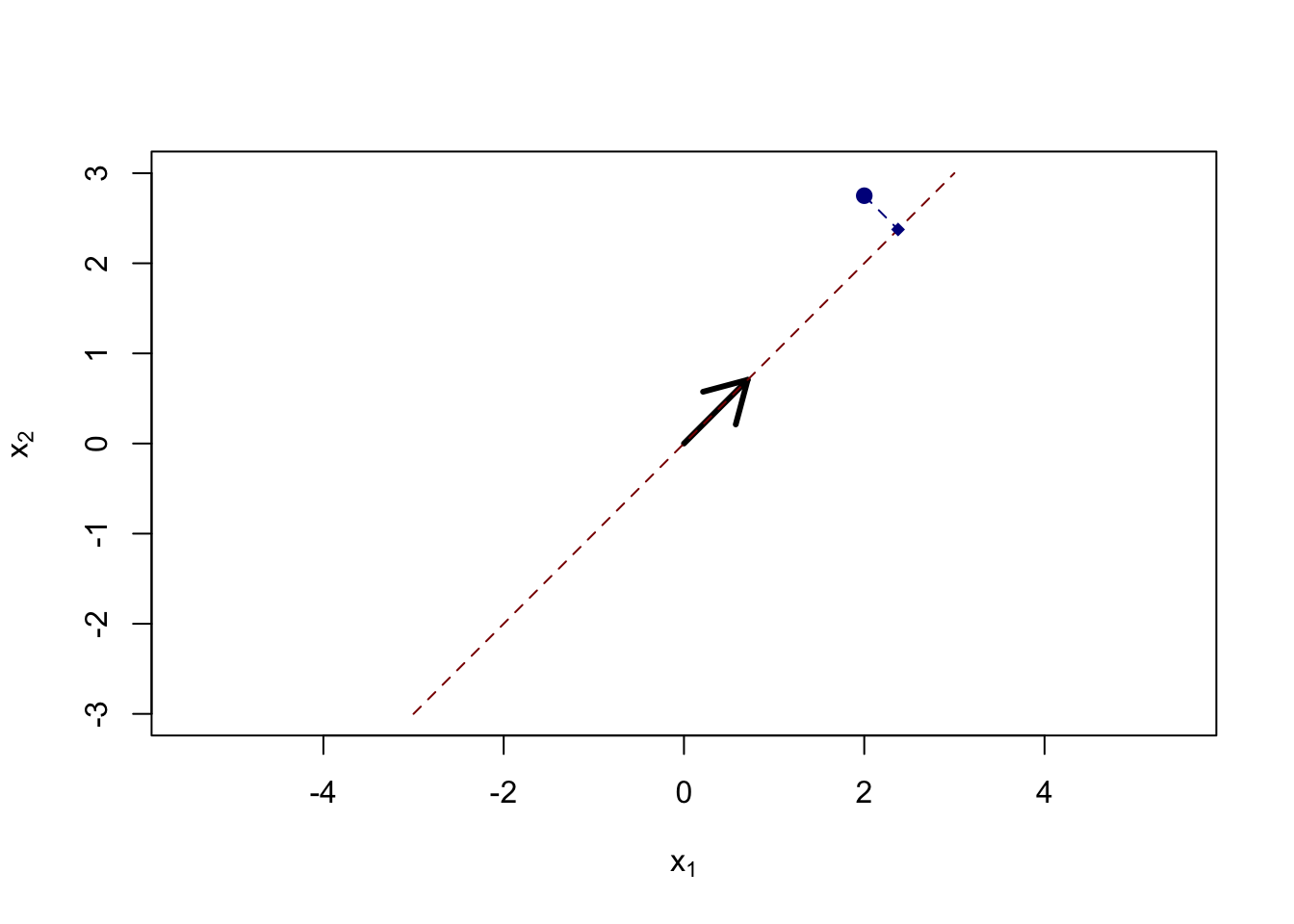
Here, we have projected the original point (big blue) to the nearest point on \(\textsf{Span}(\bv)\) (red dashed line), resulting in the DR’d smaller blue point. The ‘loss’ of this projection is measured by the Euclidean distance between the two points, here captured by the dashed blue line.

We note here that the relevant distance here is the perpendicular (straight line) distance from the original point to the target space. We do not make the \(y\)-axis special, unlike supervised learning where there is a ‘special’ response variable.

With this in hand, we are now ready to define the loss function we use to select \(v\):

\[\argmin_{\bv: \|\bv\|==1} \left\|\bx - \textsf{proj}_{\textsf{Span}(\bv)}(\bx)\right\|_2^2 = \argmin_{\bv: \|\bv\|==1} \left\|\bx - \bv \langle \bx, bv\rangle\right\|_2^2 = \argmin_{\bv: \|\bv\|==1} \left\|\bx - \bx^{\top}\bv \bv\right\|_2^2 \]

With many training points, our problem generalizes to the sum of total errors, giving us:

\[ \argmin_{\bv: \|\bv\|==1} \sum_i \left\|\bx_i - \bx^{\top}_i\bv \bv\right\|_2^2 = \argmin_{\bv: \|\bv\|==1} \left\|\bX - \bX\bv\bv^{\top}\right\|_F^2 = \argmin_{\bv: \|\bv\|==1} \left\|\bX(\bI - \bv\bv^{\top})\right\|_F^2\]

Looking at this, we see a certain similarity to OLS: we are using \(\bX\) to predict the projected \(\bX\) in a minimum MSE sense. But, unlike standard supervised learning where the response is fixed, here we get to select the response (indirectly by selecting \(\bv\)) that makes the problem as easy as possible (i.e., we get to pick the response so that the final residuals are as small as possible).

In this sense DR is a self-supervised problem: we are finding a projection that is the most predictable and looses the least amount of variance in \(\bX\). This actually ties unsupervised learning to supervised learning nicely: in supervised learning, we want to find reliable accurate predictions. In unsupervised learning, we don’t have a sense of prediction and are instead settling for finding a ‘repeatable’ pattern. But, if the pattern we find corresponds to a reliable and accurate prediction, it’s not unreasonable to assume it will generalize out-of-sample in some sense.

So how can we actually solve this problem? It’s not as clean as OLS since \(\bv\) gets ‘squared’ inside the loss (giving a fourth-degree polynomial in \(\bv\)), but it will turn out to be quite solvable anyways. If we expand our our loss, we get the following:

\[\begin{align*} \left\|\bX - \bX\bv\bv^{\top}\right\|_F^2 &= \left\|\bX\right\|_F^2 - 2 \langle \bX, \bX\bv\bv^{\top}\rangle + \left\|\bX\bv\bv^{\top}\right\|_F^2\\ &= \left\|\bX\right\|_F^2 - 2 \langle \bX, \bX\bv\bv^{\top}\rangle + \langle\bX\bv\bv^{\top}, \bX\bv\bv^{\top}\rangle\\ &= \left\|\bX\right\|_F^2 - 2 \text{Tr}(\bX^{\top}\bX\bv\bv^{\top})+ \text{Tr}((\bX\bv\bv^{\top})^{\top}(\bX\bv\bv^{\top})) \\ &= \left\|\bX\right\|_F^2 - 2 \text{Tr}(\bv^{\top}\bX^{\top}\bX\bv)+ \text{Tr}(\bv\bv^{\top}\bX^{\top}\bX\bv\bv^{\top}) \\ &= \left\|\bX\right\|_F^2 - 2 \text{Tr}(\bv^{\top}\bX^{\top}\bX\bv)+ \text{Tr}(\bv^{\top}\bX^{\top}\bX\bv\underbrace{\bv^{\top}\bv}_{=\|\bv\|^2=1}) \\ &= \left\|\bX\right\|_F^2 - 2 \text{Tr}(\bv^{\top}\bX^{\top}\bX\bv)+ \text{Tr}(\bv^{\top}\bX^{\top}\bX\bv) \\ &= \left\|\bX\right\|_F^2 - \text{Tr}(\bv^{\top}\bX^{\top}\bX\bv) \\ &= \left\|\bX\right\|_F^2 - \bv^{\top}\bX^{\top}\bX\bv \end{align*}\] Because \(\|\bX\|_F^2\) doesn’t change as a function of \(\bv\), this means our problem can be reduced to

\[\argmin_{\bv: \|\bv\|=1} - \bv^{\top}\bX^{\top}\bX\bv = \argmax_{\bv: \|\bv\|=1} \bv^{\top}\bX^{\top}\bX\bv\]

We see here that the \(\|\bv\|=1\) constraint is important: if this constraint was missing, we could simply make the objective arbitrarily large by increasing \(\bv\) without limit.

This gives us our second interpretation of our DR problem:

  1. We want to minimize the loss in projecting \(\bX\) into \(\textsf{Span}(\bv)\)
  2. We want to maximize the amount of \(\bX^{\top}\bX\) captured in the \(\bv\) direction.

At this point, it is perhaps with noting that the DR problem we have developed (in whatever form you prefer) is Principal Components Analysis (PCA).

Solving the PCA Problem with Linear Matrix Decompositions

So how can we solve the PCA problem?

\[\argmax_{\bv: \|\bv\|=1} \bv^{\top}\bX^{\top}\bX\bv\]

While you might be tempted to use the tools of convex optimization here, this isn’t actually a convex problem. In particular, we’re looking to maximize, while convex optimization normally lets us minimize. So we need to return to first principles:

We might first consider using a gradient ascent method, modifying it to maintain our \(\|\bv\|=1\) constraint. In particular, if we differentiate \(\bv^{\top}\bX^{\top}\bX\bv\) with respect to \(\bv\), we get \(2\bX^{\top}\bX\bv\), so an iteration like

\[ \bv^{(k+1)} \leftarrow \bv^{(k)} + c 2\bX^{\top}\bX\bv^{(k)} = (\bI + 2c\bX^{\top}\bX)\bv^{(k)}\]

might make sense. Rather than selecting the step size \(c\) directly, we can instead assume that we want to as far as we can without violating the \(\|\bv\|=1\) constraint and take our update to be:

\[ \bv^{(k+1)} \leftarrow \frac{(\bI + 2c\bX^{\top}\bX)\bv^{(k)}}{\|(\bI + 2c\bX^{\top}\bX)\bv^{(k)}\|}\] Note that the division here ensures \(\|\bv^{(k+1)}\}=1\) for all \(k\). Letting \(c\) be as large as possible, we can ignore that \(\bI\) term and get the simpler update:

\[ \bv^{(k+1)} \leftarrow \frac{\bX^{\top}\bX\bv^{(k)}}{\|\bX^{\top}\bX\bv^{(k)}\|}\] Because we get a result of the form \(\bv^{(k+1)} = (\bX^{\top}\bX)^{k}\bv^{(0)}\), this algorithm is sometimes known as the power method. We do not yet quite have the tools to prove that it converges to the right answer, but it usually does and is rather robust (if sometimes slow). The power method has the advantage of only requiring us to multiply by \(\bX^{\top}\bX\), so if \(\bX\) is easy to multiply by (e.g., if it is mainly 0s), our algorithm with automatically inherit any optimizations we can apply in the multiplication step.

This is an example of an iterative algorithm for PCA. It turns out that direct methods are also available using (yet another) characterization of PCA. In particular, you might recognize \(\bv\) as an eigenvalue of \(\bX^{\top}\bX\). If this isn’t immediately apparent, read on: note that, at convergence, \(\bv\) has to be a fixed point of the power iteration. That is,

\[\bv = \frac{\bX^{\top}{\bX}\bv}{\|\bX^{\top}{\bX}\bv\|}\] (If this equation weren’t satisfied, the power method would encourage us to take another step.) If we let \(\lambda = \|\bX^{\top}\bX\bv\|\), then this gives us the stationary condition:

\[\lambda \bv = \bX^{\top}{\bX}\bv\]

Note you can also get this by setting our gradient equal to zero in the original derivation to the power method, hence the (calculus-sounding) ‘stationary condition’ name.

This type of equation:

\[\textsf{scalar} * \text{vector} = \textsf{matrix} * \textsf{same vector}\]

is incredibly important in mathematics, where it is used to define the eigenvectors of a matrix. In particular, any vector that satisfies an equation of the above form is known as an eigenvector and the associated scalar is known as an eigenvector. Hence, PCA consists of finding the (leading) eigenvector-eigenvalue pair of the matrix \(\bX^{\top}\bX\).2

Eigenvectors are very well-studied and so efficient algorithms exist for finding them in almost every programming environment. In R, the eigen() function has a high-performance general purpose eigenvalue/eigenvector solver. Let’s see it in action and compare it to the power method.

n <- 500
p <- 250
X <- matrix(rnorm(n * p), nrow=n)
XtX <- crossprod(X)

## Power method
normalize <- function(v) v / sqrt(sum(v^2))
v <- matrix(rnorm(p), ncol=1); v <- normalize(v)

system.time({
    repeat {
        v_old <- v
        v <- normalize(XtX %*% v)
        
        if(sum(abs(v - v_old)) < 1e-10) break
    }
})
   user  system elapsed 
  0.076   0.001   0.077 
v_pm <- v
lambda_pm <- mean((XtX %*% v_pm) / v_pm)

## eigen()
system.time({eigen_decomp <- eigen(XtX, symmetric=TRUE)})
   user  system elapsed 
  0.013   0.001   0.015

So here the optimized algorithm is about 10x faster. But it’s actually much more impressive than that. If you look at eigen_decomp, you’ll see it actually computed all 250 eigenpairs, not just the one we are interested in, so it’s really more like 2500 times faster.

To wit,

all.equal(eigen_decomp$value[1], 
          lambda_pm)
[1] TRUE
all.equal(eigen_decomp$vectors[,1,drop=FALSE], +v_pm)
[1] TRUE
all.equal(eigen_decomp$vectors[,1,drop=FALSE], -v_pm)
[1] "Mean relative difference: 2"

Here we compare against both \(\pm \bv\) since the eigenvalue is only defined up to sign (recall from our picture above where we can ‘flip’ the seed direction but the span is unchanged) but R isn’t smart enough to know the difference so we have to help it out a bit.

For small to medium problems, it is usually a good idea to use built-in algorithms like eigen or (as we will see below) svd. For very large problems, it may be better to use the power method (or similar) as it only computes the first eigenvector. As you will see in RR#03, the power method is also quite easy to extend if we want to introduce sparsity or similar forms of regularization.

Additional Principal Components

So far, we have done extreme dimension reduction all the way from \(\R^P\) down to \(\R^1\). We have found that the eigenvectors of \(\bX^{\top}\bX\) give us a way to do this optimally, but that’s still a huge (and unavoidable) loss of information. What if we want to reduce only to \(\R^2\) or \(\R^3\) (or generally \(\R^p\) for \(P \gg p > 1\))? We expect that this additional dimension (or ‘additional degree of freedom’) will help us, but by how much? And how can we best take advantage of it?

To go down this path, we need to look at one form of our decomposition from above:

\[\argmin_{\bv: \|\bv\|=1} \|\bX(\bI - \bv\bv^{\top})\|_F^2\]

This quantity – \(\bR = \bX(\bI - \bv\bv^{\top})\) – plays the role of residuals for PCA; it is all of the data ‘left-over’ after we project onto \(\bv\). By definition, there will be no \(\bv\) left in this residual, as we can see:

\[\bR\bv = \bX(\bI - \bv\bv^{\top})\bv = \bX(\bv - \bv\bv^{\top}\bv) = \bX(\bv - \bv) = \bzero\]

This suggests to us that, if we want to use our new second dimension smartly, it will not have anything to do with \(\bv\). In particular, we might expect it to be orthogonal to \(\bv\) (and it turns out - we would be right!).

We can start with a rather naive approach: what if we just get “the best of the rest” and perform PCA again on \(\bR\). The resulting vector \(\bv_2\) will capture something in \(\bR\) (hopefully a large part of it) and, because \(\bR\) has only variance orthogonal to \(\bv_1\), it will add something new to our decomposition.

Formally, this approach is known as deflation: we perform PCA first on \(\bX\), then on \(\bR_1 = \bX(\bI - \bv_1\bv_1^{\top})\), then on \(\bR_2 = \bR_1(\bI - \bv_2\bv_2^{\top})\), etc. The coefficients in the resulting space are given by

\[(\bX\bv_1, \bX\bv_2, \dots)\]

We can see this in action visually:

library(plotly)

S <- matrix(c(16, -8, -2, 
              -8, 22, 10, 
              -2, 10, 25), nrow=3, byrow=TRUE)

library(MASS)

X <- mvrnorm(5000, Sigma=S, mu=c(0, 0, 0))

plot_ly(x=X[,1], y=X[,2], z=X[,3], 
        type="scatter3d", mode="markers") |>
    layout(title="Original 3D Data Set")

Here, we have generated \(n=5000\) points in \(\R^3\). Because our feature are not uncorrelated, the resulting point cloud is not quite spherical. If we perform PCA on this data, the one dimensional projection of our results is rather uninteresting:

pca_power_method <- function(X, thresh=1e-8){
    XtX <- crossprod(X)
    p <- NCOL(XtX)
    normalize <- function(x) x / sqrt(sum(x^2))
    
    v <- normalize(matrix(rnorm(p), ncol=1))
    
    repeat {
        v_old <- v
        v <- normalize(XtX %*% v)
        
        # To fix sign irregularity, force v[1] > 0
        if(v[1] < 0) v <- -v
        
        if(sum(abs(v - v_old)) < thresh){
            break
        }
    }
    
    list(v=v, lambda=sqrt(sum((XtX %*% v)^2)))
}

PC1 <- pca_power_method(X)

X_pc1 <- X %*% PC1$v

plot(X_pc1)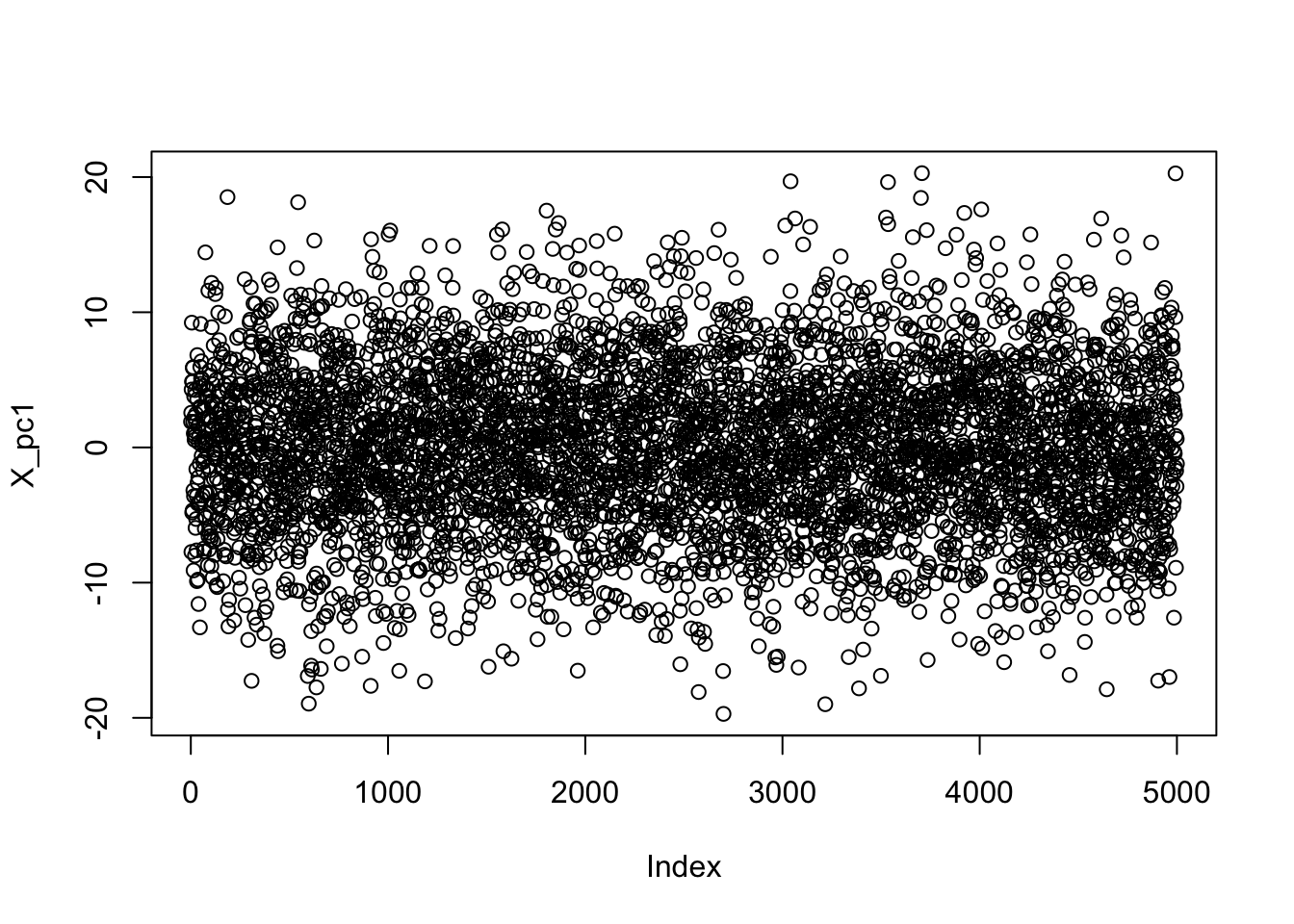

As we might expect for this IID data, there’s no meaningful structure here. The residuals on the other hand (\(\bR_1\)) are somewhat interesting:

eye <- function(n) diag(1, n, n)
R1 <- X %*% (eye(3) - tcrossprod(PC1$v))

plot_ly(x=R1[,1], y=R1[,2], z=R1[,3], 
        type="scatter3d", mode="markers") |>
    layout(title="Residuals after removing 1 PC")

If you rotate this data in just the right way, you will see that it is flat along one dimension. And if you look even closer, you will see that the flat dimension is exactly \(\bv_1\) - that is, the direction we first found in PCA. This makes sense - we “pulled out” \(\bv_1\) in forming \(\bR_1\), so there is no \(\bv_1\) left in our residuals.

At this point, we can benefit from introducing another important linear algebra concept: rank. The rank of a matrix (i.e., of a point cloud) is the number of dimensions it ‘actually’ occupies. Our original data was rank-3, since it used all three dimensions of our data space, but the residuals \(\bR_1\) are only rank-2, since we removed one dimension. You can think of rank as the “intrinsic dimension” associated with data.

v1 <- matrix(c(-1/3, 2/3, 2/3), ncol=1)

X_projection1 <- X %*% v1

X_residuals <- X - X %% v1 %% t(v1)

plot_ly(x=X_residuals[,1], y=X_residuals[,2], z=X_residuals[,3], type=“scatter3d”, mode=“markers”)

v2 <- matrix(c(2/3, -1/3, 2/3), ncol=1)

X_residuals_projection1 <- X_residuals %*% v2

X_resid_resid <- X_residuals - X_residuals %% v2 %% t(v2)

X_residuals (I - v1 %% t(v1) - v2 %% t(v2))

plot_ly(x=X_resid_resid[,1], y=X_resid_resid[,2], z=X_resid_resid[,3], type=“scatter3d”, mode=“markers”)

Visualizing PCA

A Singular Value Approach to PCA

Regularized PCA

Other Applications of PCA-Type Decompositions

Footnotes

  1. Later, we will use a more generalized notion of ‘dimension’, leading us to the task of manifold learning.↩︎

  2. A matrix of size \(p \times p\) can have up to \(p\) eigenvalue-eigenvector pairs. Because we are maximizing \(\bv^{\top}\bX^{\top}\bX\bv\), we want the maximal (or leading) eigenvector-eigenvalue pair, defined as the one for which the (absolute value of) the eigenvalue is the largest.↩︎