Splitting Methods for Convex Bi-Clustering and Co-Clustering
Abstract: Co-Clustering, the problem of simultaneously identifying clusters across multiple aspects of a data set, is a natural generalization of clustering to higher-order structured data. Recent convex formulations of bi-clustering and tensor co-clustering, which shrink estimated centroids together using a convex fusion penalty, allow for global optimality guarantees and precise theoretical analysis, but their computational properties have been less well studied. In this note, we present three efficient operator-splitting methods for the convex co-clustering problem: a standard two-block ADMM, a Generalized ADMM which avoids an expensive tensor Sylvester equation in the primal update, and a three-block ADMM based on the operator splitting scheme of Davis and Yin. Theoretical complexity analysis suggests, and experimental evidence confirms, that the Generalized ADMM is far more efficient for large problems.
Publisher DOI: 10.1109/DSW.2019.8755599
Working Copy: ArXiv 1901.06075
Summary: Chi and Lange (J. Computational and Graphical Statistics, 2015) established that splitting methods are an easy-to-implement highly-performant way to solve convex clustering problems. In this work, I extend their analysis to the general case of tensor co-clustering, considering three operator-splitting schemes:
- The classic ADMM
- A generalized (quadratically perturbed) ADMM
- Davis-Yin splitting (equivalent to AMA for this problem)
Classical ADMM has the best per iteration performance, but requires solving a (tensor) Sylvester equation at each iteration, which is typically prohibitive. To avoid this, I construct a generalized ADMM scheme that avoids any matrix decompositions or inverses in the updates.
\[\begin{align*} \mathbf{U}^{(k+1)} &= \left(\alpha \mathbf{U}^{(k)} + \mathbf{X} + \rho\mathbf{D}_{\text{row}}^T(\mathbf{V}^{(k)} - \rho^{-1}\mathbf{Z}^{(k)}_{\text{row}} - \mathbf{D}_{\text{row}}\mathbf{U}^{(k)}) \right. \\ &\left.\qquad+ \rho(\mathbf{V}^{(k)}_{\text{col}} - \rho^{-1}\mathbf{Z}^{(k)}_{\text{col}} - \mathbf{U}^{(k)}\mathbf{D}_{\text{col}})\mathbf{D}_{\text{col}}^T \right)/(1+\alpha) \\ \begin{pmatrix} \mathbf{V}^{(k+1)}_{\text{row}} \\ \mathbf{V}^{(k+1)}_{\text{col}} \end{pmatrix} &= \begin{pmatrix} \text{prox}_{\lambda / \rho \|\cdot\|_{\text{row}, q}}(\mathbf{D}_{\text{row}}\mathbf{U}^{(k+1)} + \rho^{-1}\mathbf{Z}^{(k)}_{\text{row}}) \\ \text{prox}_{\lambda / \rho \|\cdot\|_{\text{col}, q}}(\mathbf{U}^{(k+1)}\mathbf{D}_{\text{col}} + \rho^{-1}\mathbf{Z}^{(k)}_{\text{col}}) \end{pmatrix} \\ \begin{pmatrix} \mathbf{Z}^{(k+1)}_{\text{row}} \\ \mathbf{Z}^{(k+1)}_{\text{col}} \end{pmatrix} &= \begin{pmatrix} \mathbf{Z}^{(k)}_{\text{row}} + \rho(\mathbf{D}_{\text{row}}\mathbf{U}^{(k+1)} - \mathbf{V}^{(k+1)}_{\text{row}}) \\ \mathbf{Z}^{(k)}_{\text{col}} + \rho(\mathbf{U}^{(k+1)}\mathbf{D}_{\text{col}} - \mathbf{V}^{(k+1)}_{\text{col}}) \end{pmatrix} \end{align*}\] This method has slightly worse per iteration performance, but has superior wall clock performance and better computational complexity.
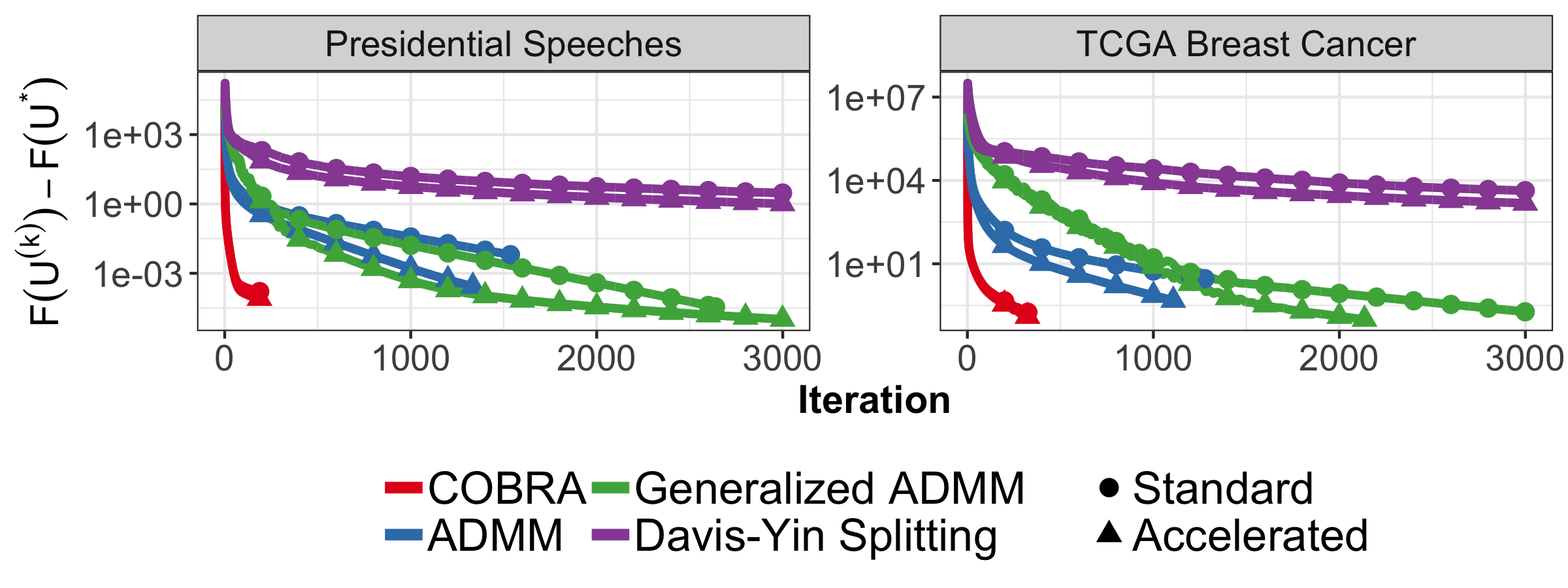
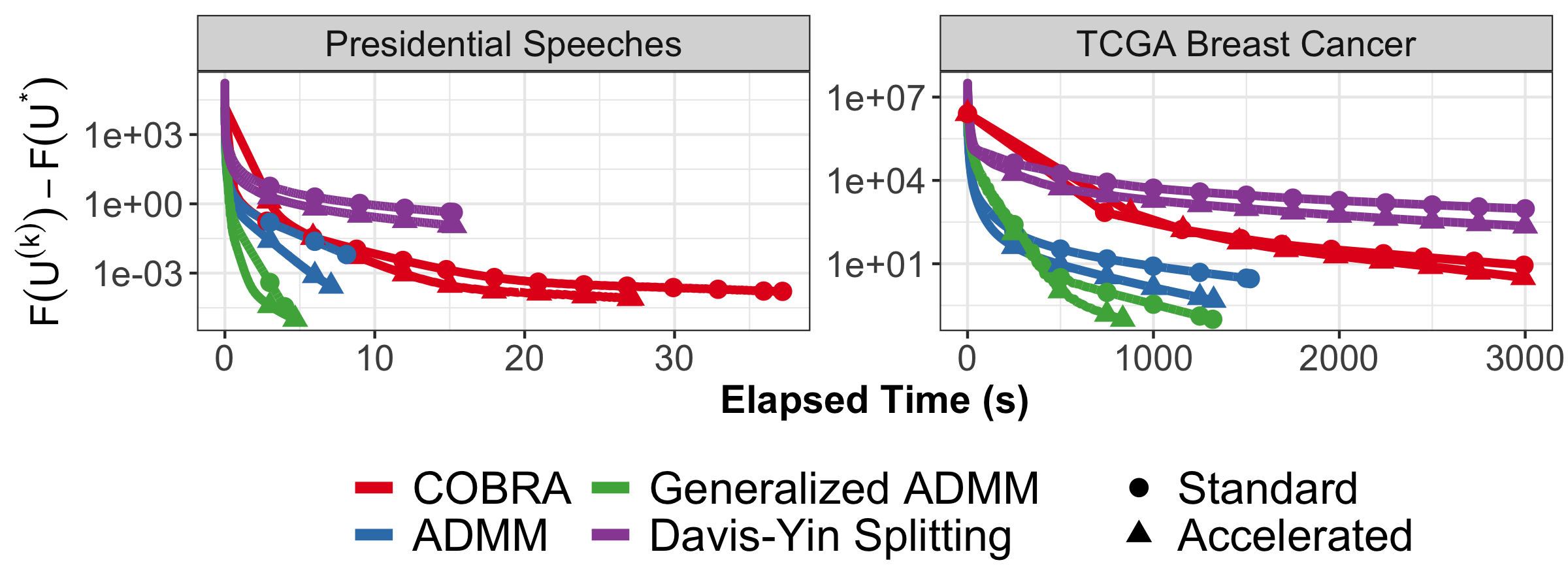
The generalized ADMM is used internally in my clustRviz software for both the exact solver and the CBASS pathwise algorithm.
Related Software: clustRviz
Citation:
@INPROCEEDINGS{Weylandt:2019-BiClustering,
TITLE="Splitting Methods for Convex Bi-Clustering and Co-Clustering",
AUTHOR="Michael Weylandt",
CROSSREF={DSW:2019},
DOI="10.1109/DSW.2019.8755599",
PAGES={237-244}
}
@PROCEEDINGS{DSW:2019,
BOOKTITLE="{DSW} 2019: Proceedings of the 2\textsuperscript{nd} {IEEE} Data Science Workshop",
YEAR=2019,
EDITOR="George Karypis and George Michailidis and Rebecca Willett",
PUBLISHER="{IEEE}",
LOCATION="Minneapolis, Minnesota"
}