Sparse and Functional Principal Components Analysis

DSW 2019: Proceedings of the IEEE Data Science Workshop 2019, pp.11-16. 2019.

Authors

Affiliations

Departments of Electrical & Computer Engineering, Computer Science, and Statistics, Rice University

Department of Statistics, Rice University

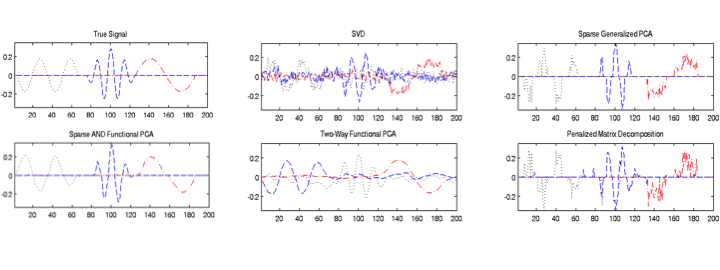
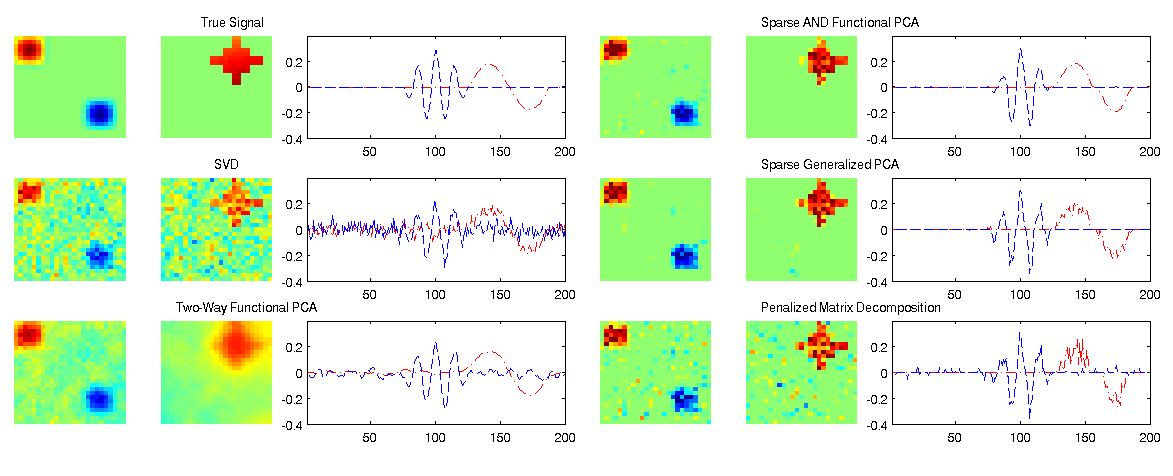
Abstract: Regularized variants of Principal Components Analysis, especially Sparse PCA and Functional PCA, are among the most useful tools for the analysis of complex high-dimensional data. Many examples of massive data, have both sparse and functional (smooth) aspects and may benefit from a regularization scheme that can capture both forms of structure. For example, in neuro-imaging data, the brain’s response to a stimulus may be restricted to a discrete region of activation (spatial sparsity), while exhibiting a smooth response within that region. We propose a unified approach to regularized PCA which can induce both sparsity and smoothness in both the row and column principal components. Our framework generalizes much of the previous literature, with sparse, functional, two-way sparse, and two-way functional PCA all being special cases of our approach. Our method permits flexible combinations of sparsity and smoothness that lead to improvements in feature selection and signal recovery, as well as more interpretable PCA factors. We demonstrate the efficacy of our method on simulated data and a neuroimaging example on EEG data.

Publisher DOI: 10.1109/DSW.2019.8755778

Working Copy: ArXiv 1309.2895

Summary: We give a unified proposal for regularized PCA, allowing for both sparsity and smoothness (functional structure) in both the estimated observation and feature embeddings (left and right singular values): [{ ^n{{}}, ^p{{}}} ^T - {} P_{}() - {} P{}()] Our approach incorporates a variety of prior proposals as special cases, including:

Classical (Unregularized) PCA
One-Way Sparse PCA: Shen and Huang (J. Multivariate Analysis, 2008)
Two-Way Sparse PCA: Allen, Grosenick, and Taylor (J. American Statistical Association, 2014) and Witten, Tibshirani, and Hastie (Biostatistics, 2009)
One-Way Functional PCA: Silverman (Annals of Statistics, 1996) and Huan, Shen, and Buja (Electronic Journal of Statistics, 2008)
Two-Way Functional PCA: Huang, Shen, and Buja (J. American Statistical Association, 2009)

We prove that our proposal is well-formulated, i.e., that all constraints are either binding or clearly slack with no masking, and give an efficient algorithm for finding a Nash point of the non-convex SFPCA problem. Finally, we apply our result in simulations and to EEG data and show that it finds meaningful and useful principal components.

The ArXiv-only appendices of this paper have quite a lot of useful content, including detailed analysis of the SFPCA problem and equivalencies to other regularized PCA schemes. Appendix C gives a thorough review of the regularized PCA literature as of 2019.

*In Silico* Comparison of SFPCA with other PCA Variants

Recovering space-time localized left and right singular vectors with SFPCA

Related Software: MoMA

Citation:

@INPROCEEDINGS{Allen:2019,
  TITLE="Sparse and Functional Principal Components Analysis",
  AUTHOR="Genevera I. Allen and Michael Weylandt",
  CROSSREF={DSW:2019},
  DOI="10.1109/DSW.2019.8755778",
  PAGES={11-16}
}

@PROCEEDINGS{DSW:2019,
  TITLE="{DSW} 2019: Proceedings of the 2\textsuperscript{nd} {IEEE} Data Science Workshop",
  YEAR=2019,
  EDITOR="George Karypis and George Michailidis and Rebecca Willett",
  PUBLISHER="{IEEE}",
  LOCATION="Minneapolis, Minnesota"
}