Automatic Registration and Convex Clustering of Time Series
Abstract: Clustering of time series data exhibits a number of challenges not present in other settings, notably the problem of registration (alignment) of observed signals. Typical approaches include pre-registration to a user-specified template or time warping approaches which attempt to optimally align series with a minimum of distortion. For many signals obtained from recording or sensing devices, these methods may be unsuitable as a template signal is not available for pre-registration, while the distortion of warping approaches may obscure meaningful temporal information. We propose a new method for automatic time series alignment within a clustering problem. Our approach, Temporal Registration using Optimal Unitary Transformations (TROUT), is based on a novel dissimilarity measure between time series that is easy to compute and automatically identifies optimal alignment between pairs of time series. By embedding our new measure in a optimization formulation, we retain well-known advantages of computational and statistical performance. We provide an efficient algorithm for TROUT-based clustering and demonstrate its superior performance over a range of competitors.
Publisher DOI: 10.1109/ICASSP39728.2021.9414417
Working Copy: ArXiv 2012.04756
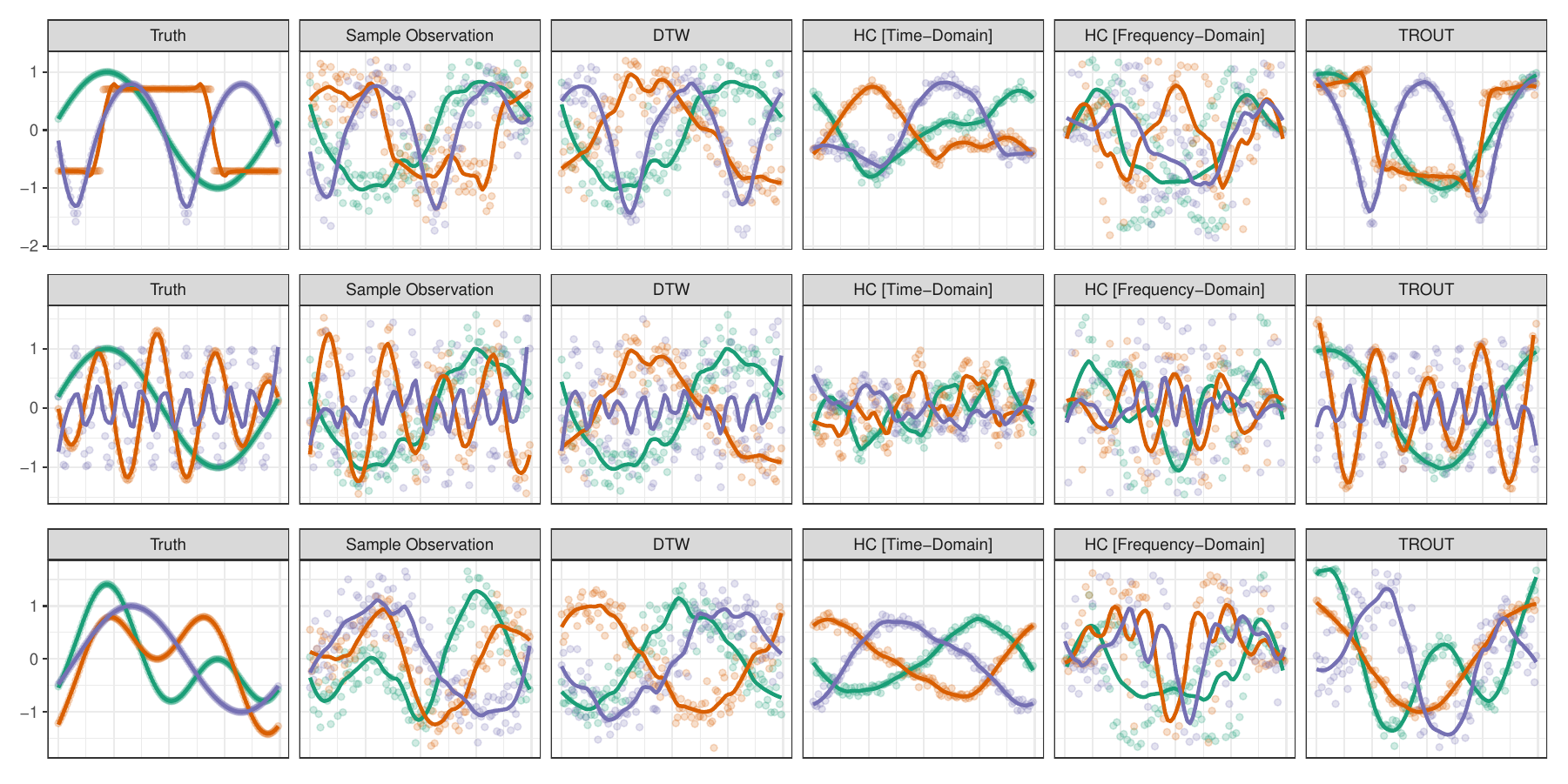
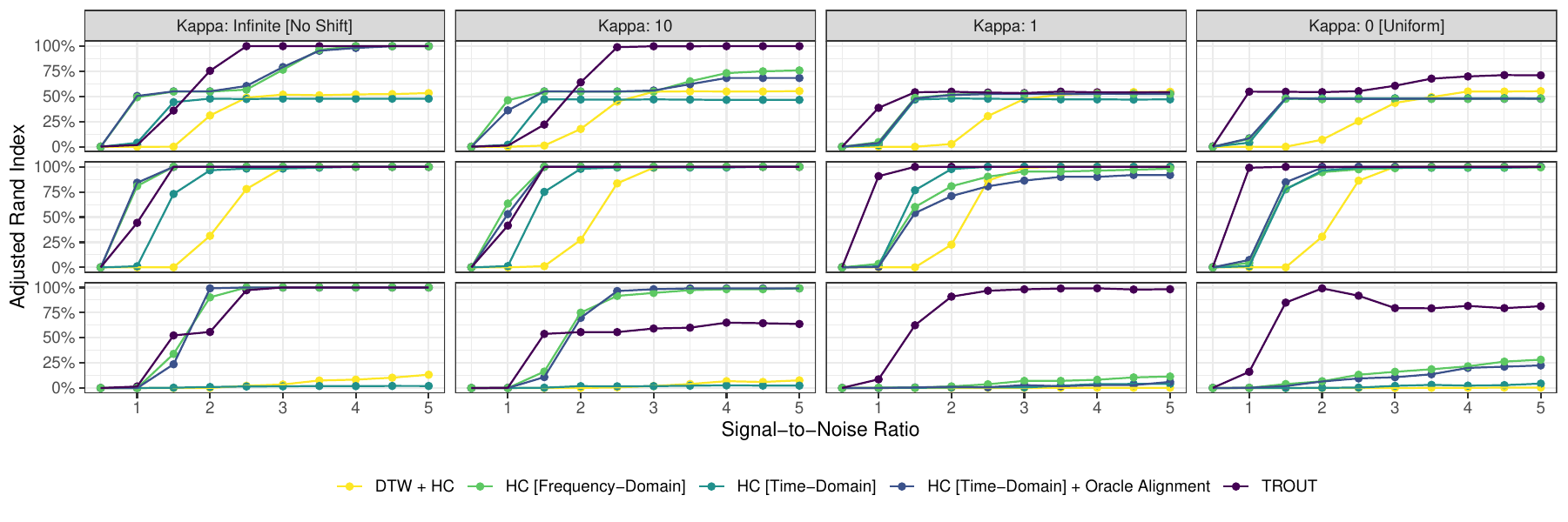
Summary: Clustering time series is a common problem in many applications, but it is much more difficult when analyzing non-aligned signals. Typically, signals are pre-registered to some template or common alignment, but this assumes that such a template exists, when discovering “standard signals” is often the goal of clustering in the first case. We instead propose to align signals to each other within the clustering problem. Given two signals, the optimal alignment between them can be found by an orthogonal rotation (phase-shift), with closed form: this motivates TROUT-clustering [{ ^{n p}} d{}(, )^2 + {}^n w{ij} |{i} - {j}|q] where [d{}(, ) = _{To solve this problem, we develop a Majorization-Minimization scheme, the sub-problems of which have closed form solution, yielding an efficient algorithm.
Note that the clustering formulation is designed so that each observation (row of \(\mathbf{X}\)) is rotated to coincide with the shared centroids (row of \(\mathbf{U}\)) rather than to each other: this avoids the registration problem entirely, but does give a solution that is only identified up to phase. Our method performs well under a variety of noise conditions and often even out-performs traditional clustering methods with oracle pre-registration.
Citation:
@INPROCEEDINGS{Weylandt:2021-TROUT,
AUTHOR="Michael Weylandt and George Michailidis",
TITLE="Automatic Registration and Convex Clustering of Time Series",
DOI="10.1109/ICASSP39728.2021.9414417"
PAGES={5609-5613},
CROSSREF="ICASSP:2021"
}
@PROCEEDINGS{ICASSP:2021,
BOOKTITLE="ICASSP 2021: Proceedings of the 2021 IEEE International Conference on Acoustics, Speech and Signal Processing",
YEAR=2021,
LOCATION="Toronto, Canada"
EDITOR="Tim Davidson and Dong Yu"
}