R
Due Date: 2025-12-03 (Wednesday) at 11:59pm
Submission: CUNY Brightspace
In our final week, we are going to look into predictive modeling (i.e., black-box machine learning) with R. Specifically, we are going to introduce the tidymodels framework in class, which provides a consistent toolkit for interacting with a wide range of modeling tools. Before we get to tidymodels, it will be useful to remember the basic modeling functionality in “basic R”.
You have hopefully seen some of this material previously in your STA 9708 or STA 9700 courses. If you haven’t, the mathematical details of what are happening here are not important for our purposes and I’d encourage you to focus on the code and user-interface instead.
R
When studying dplyr, we performed many comparisons between penguin groups: e.g.,
library(tidyverse)
penguins |>
drop_na() |>
group_by(species) |>
summarize(mean_body_mass = mean(body_mass))# A tibble: 3 × 2
species mean_body_mass
<fct> <dbl>
1 Adelie 3706.
2 Chinstrap 3733.
3 Gentoo 5092.While we can compute the difference in averages,1 we may reasonably ask whether this difference rises to the level of statistical significance: that is, is there enough evidence to say that there is a systematic difference, or could the difference be plausibly due to getting a few extra-chunky penguins?
This type of statistical question is a deep and fundamental part of statistics, generally known as inference, and it is a topic you will cover at great length in your other courses. In this note, we simply focus on the computational steps needed to perform tests.
We will implement two of the most widely used types of tests here, though many others can be implemented using the same framework.
For each of these, we will make use of the infer package, though base R equivalents are available.
Perhaps the most fundamental task in statistics is to ask whether two groups are systematically different: this is the world of two-sample testing. ‘Systematically different’ is a somewhat slippery term requiring more more specificity: if we interpret it to mean “having different means”, then we arrive at so-called \(t\)-tests: tests of whether two groups have different means.
\(t\)-tests are typically performed under the assumption that each observation is normally distributed around its groups respective mean. This assumption, like most normality assumptions, is impossible to verify, but the magic of statistics is that – with enough data in conditions that aren’t too terrible2 – this is often a reasonable assumption to make. When we assume normality, the distribution of the estimated difference in means divided by the estimated standard deviation follows a \(t\)-distribution, giving this test its name.
With the infer package, this type of test is implemented with the t_test function.3 Like most tidyverse functions, the first argument to this function is a data frame. The second argument is a formula: we haven’t done much with formulas to this point, but you might remember them from facet_grid in ggplot2.
A formula is an expression with a variable name on each side separated by a ~.4 Conventionally, the variable on the left-hand side is the response and the variable on the right-hand side is the explanatory variable. In a \(t\)-test, the response is the quantity we care about, while the explanatory variable is the group identifier.5 So, for our beloved penguins, if we want to see if males weigh more than females, we would use the formula:
body_mass ~ sexThis gives us:
Warning: The statistic is based on a difference or ratio; by default, for
difference-based statistics, the explanatory variable is subtracted in the
order "female" - "male", or divided in the order "female" / "male" for
ratio-based statistics. To specify this order yourself, supply `order =
c("female", "male")`.# A tibble: 1 × 7
statistic t_df p_value alternative estimate lower_ci upper_ci
<dbl> <dbl> <dbl> <chr> <dbl> <dbl> <dbl>
1 -8.55 324. 4.79e-16 two.sided -683. -841. -526.Note the warning message here: we are looking at the difference in groups, but we have not said which groups or in what order to compare them. Following the text of the warning, it is a good idea to specify the order of the comparisons:
# A tibble: 1 × 7
statistic t_df p_value alternative estimate lower_ci upper_ci
<dbl> <dbl> <dbl> <chr> <dbl> <dbl> <dbl>
1 8.55 324. 4.79e-16 two.sided 683. 526. 841.By specifing the order in this manner, we indicate that we are looking at the average male body mass minus the average female body mass. As such, most of our results are flipped in sign from what we saw before.
Let’s look at the columns of our result:
estimate: this is our best guess (“point estimate”) of the inter-group differencelower_ci and upper_ci: these are the lower and upper end points of a confidence interval for our estimate. By default, these are set at the conventional 95% level, but this can be changed by supplying the conf_level argument. (Test yourself: if we set conf_level=0.9 instead, what would happen to these two values?)p_value: This is a \(p\)-value, indicating the strength of evidence against the null hypothesis that the averages of the two groups are equal. Smaller \(p\)-values indicate more confidence that there is a systematic difference.alternative: This is honestly a bit odd, but functionally, it is an indirect way of specifying the null hypothesis tested. Here, the two.sided alternative, indicates that we tested a null of equality. If a directional alternative was provided (e.g., "greater"), we would have tested against a null of “less than or equal”.6
The use of a data.frame here means that infer plays nicely with the tools we have been using all semester long. For instance, we might question whether all penguin species have an inter-sex difference: to test this, we split our data into three parts and test them separately:
penguins |>
group_by(species) |>
nest() |>
mutate(test_results = map(data, t_test, body_mass ~ sex, order=c("male", "female"))) |>
unnest(test_results) |>
arrange(desc(estimate))# A tibble: 3 × 9
# Groups: species [3]
species data statistic t_df p_value alternative estimate lower_ci
<fct> <list> <dbl> <dbl> <dbl> <chr> <dbl> <dbl>
1 Gentoo <tibble> 14.8 117. 1.87e-28 two.sided 805. 697.
2 Adelie <tibble> 13.1 136. 6.40e-26 two.sided 675. 573.
3 Chinstrap <tibble> 5.21 62.6 2.26e- 6 two.sided 412. 254.
# ℹ 1 more variable: upper_ci <dbl>Here, we see that Gentoos, being the largest penguins in our data, exhibit the largest sex difference. This pattern can be very useful for testing sub-group differences, though you should take at least a bit of care to avoid issues with multiplicity corrections:
This structure plays particularly nicely with ggplot2 for visualizing differences:
penguins |>
group_by(species) |>
nest() |>
mutate(test_results = map(data, t_test, body_mass ~ sex, order=c("male", "female"))) |>
unnest(test_results) |>
ggplot(aes(x=species,
y=estimate,
ymax=upper_ci,
ymin=lower_ci)) +
geom_point(size=4) +
geom_errorbar() +
xlab("Species") +
ylab("Estimated Sex Difference in Mean Body Mass") +
theme_bw()
The prop_test function extends this paradigm to the case where the response is a binary variable. This analysis is conceptually quite similar to a \(t\)-test, but the mathematical details are based on a binomial distribution, not a normal distribution.
penguins |>
drop_na() |>
mutate(is_male = (sex == "male"),
is_gentoo = (species == "Gentoo")) |>
prop_test(is_male ~ is_gentoo, order=c("TRUE", "FALSE"))# A tibble: 1 × 6
statistic chisq_df p_value alternative lower_ci upper_ci
<dbl> <dbl> <dbl> <chr> <dbl> <dbl>
1 0.0113 1 0.915 two.sided -0.106 0.131Notice here that we constructed our binary variables (is_male, is_gentoo) manually. In theory, you can pass categorical variables to prop_test directly and it will binarize them for you, but I find that behavior a bit too fragile.
In both of these tests, we can instead perform a “one-sample” test, by not specifying an explanatory variable and instead passing NULL
penguins |>
mutate(is_male = (sex == "male")) |>
prop_test(is_male ~ NULL, order=c("TRUE", "FALSE"))No `p` argument was hypothesized, so the test will assume a null hypothesis `p
= .5`.# A tibble: 1 × 6
statistic chisq_df p_value alternative lower_ci upper_ci
<dbl> <int> <dbl> <chr> <dbl> <dbl>
1 0.0120 1 0.913 two.sided 0.450 0.559Here, as the message suggests, we are testing against a null that the population rate is 50% (equal male and female). We can specify p for other nulls:
penguins |>
mutate(is_male = (sex == "male")) |>
prop_test(is_male ~ NULL, order=c("TRUE", "FALSE"),
p=0.6666)# A tibble: 1 × 4
statistic chisq_df p_value alternative
<dbl> <int> <dbl> <chr>
1 38.6 1 5.09e-10 two.sided So (unsurprisingly), we can say with high-confidence that there are not twice as many male penguins as females in our sample.
R
Another important task for which R is well suited is the fitting and usage of statistical models. As noted above, we will consider this topic in detail in class, but it is worth being familiar with the basic tool for fitting linear models in R, the lm function.
The tidymodels package includes the ames data set, which records 82 variables about 2,930 properties sold in Ames, Iowa. Clearly, predicting the sale price of these properties is of significant interest, but with so many variables of different types, this is a non-trivial modeling challenges:
library(tidyverse)
library(tidymodels)
glimpse(ames)Rows: 2,930
Columns: 74
$ MS_SubClass <fct> One_Story_1946_and_Newer_All_Styles, One_Story_1946…
$ MS_Zoning <fct> Residential_Low_Density, Residential_High_Density, …
$ Lot_Frontage <dbl> 141, 80, 81, 93, 74, 78, 41, 43, 39, 60, 75, 0, 63,…
$ Lot_Area <int> 31770, 11622, 14267, 11160, 13830, 9978, 4920, 5005…
$ Street <fct> Pave, Pave, Pave, Pave, Pave, Pave, Pave, Pave, Pav…
$ Alley <fct> No_Alley_Access, No_Alley_Access, No_Alley_Access, …
$ Lot_Shape <fct> Slightly_Irregular, Regular, Slightly_Irregular, Re…
$ Land_Contour <fct> Lvl, Lvl, Lvl, Lvl, Lvl, Lvl, Lvl, HLS, Lvl, Lvl, L…
$ Utilities <fct> AllPub, AllPub, AllPub, AllPub, AllPub, AllPub, All…
$ Lot_Config <fct> Corner, Inside, Corner, Corner, Inside, Inside, Ins…
$ Land_Slope <fct> Gtl, Gtl, Gtl, Gtl, Gtl, Gtl, Gtl, Gtl, Gtl, Gtl, G…
$ Neighborhood <fct> North_Ames, North_Ames, North_Ames, North_Ames, Gil…
$ Condition_1 <fct> Norm, Feedr, Norm, Norm, Norm, Norm, Norm, Norm, No…
$ Condition_2 <fct> Norm, Norm, Norm, Norm, Norm, Norm, Norm, Norm, Nor…
$ Bldg_Type <fct> OneFam, OneFam, OneFam, OneFam, OneFam, OneFam, Twn…
$ House_Style <fct> One_Story, One_Story, One_Story, One_Story, Two_Sto…
$ Overall_Cond <fct> Average, Above_Average, Above_Average, Average, Ave…
$ Year_Built <int> 1960, 1961, 1958, 1968, 1997, 1998, 2001, 1992, 199…
$ Year_Remod_Add <int> 1960, 1961, 1958, 1968, 1998, 1998, 2001, 1992, 199…
$ Roof_Style <fct> Hip, Gable, Hip, Hip, Gable, Gable, Gable, Gable, G…
$ Roof_Matl <fct> CompShg, CompShg, CompShg, CompShg, CompShg, CompSh…
$ Exterior_1st <fct> BrkFace, VinylSd, Wd Sdng, BrkFace, VinylSd, VinylS…
$ Exterior_2nd <fct> Plywood, VinylSd, Wd Sdng, BrkFace, VinylSd, VinylS…
$ Mas_Vnr_Type <fct> Stone, None, BrkFace, None, None, BrkFace, None, No…
$ Mas_Vnr_Area <dbl> 112, 0, 108, 0, 0, 20, 0, 0, 0, 0, 0, 0, 0, 0, 0, 6…
$ Exter_Cond <fct> Typical, Typical, Typical, Typical, Typical, Typica…
$ Foundation <fct> CBlock, CBlock, CBlock, CBlock, PConc, PConc, PConc…
$ Bsmt_Cond <fct> Good, Typical, Typical, Typical, Typical, Typical, …
$ Bsmt_Exposure <fct> Gd, No, No, No, No, No, Mn, No, No, No, No, No, No,…
$ BsmtFin_Type_1 <fct> BLQ, Rec, ALQ, ALQ, GLQ, GLQ, GLQ, ALQ, GLQ, Unf, U…
$ BsmtFin_SF_1 <dbl> 2, 6, 1, 1, 3, 3, 3, 1, 3, 7, 7, 1, 7, 3, 3, 1, 3, …
$ BsmtFin_Type_2 <fct> Unf, LwQ, Unf, Unf, Unf, Unf, Unf, Unf, Unf, Unf, U…
$ BsmtFin_SF_2 <dbl> 0, 144, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1120, 0…
$ Bsmt_Unf_SF <dbl> 441, 270, 406, 1045, 137, 324, 722, 1017, 415, 994,…
$ Total_Bsmt_SF <dbl> 1080, 882, 1329, 2110, 928, 926, 1338, 1280, 1595, …
$ Heating <fct> GasA, GasA, GasA, GasA, GasA, GasA, GasA, GasA, Gas…
$ Heating_QC <fct> Fair, Typical, Typical, Excellent, Good, Excellent,…
$ Central_Air <fct> Y, Y, Y, Y, Y, Y, Y, Y, Y, Y, Y, Y, Y, Y, Y, Y, Y, …
$ Electrical <fct> SBrkr, SBrkr, SBrkr, SBrkr, SBrkr, SBrkr, SBrkr, SB…
$ First_Flr_SF <int> 1656, 896, 1329, 2110, 928, 926, 1338, 1280, 1616, …
$ Second_Flr_SF <int> 0, 0, 0, 0, 701, 678, 0, 0, 0, 776, 892, 0, 676, 0,…
$ Gr_Liv_Area <int> 1656, 896, 1329, 2110, 1629, 1604, 1338, 1280, 1616…
$ Bsmt_Full_Bath <dbl> 1, 0, 0, 1, 0, 0, 1, 0, 1, 0, 0, 1, 0, 1, 1, 1, 0, …
$ Bsmt_Half_Bath <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, …
$ Full_Bath <int> 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 1, 1, 3, 2, …
$ Half_Bath <int> 0, 0, 1, 1, 1, 1, 0, 0, 0, 1, 1, 0, 1, 1, 1, 1, 0, …
$ Bedroom_AbvGr <int> 3, 2, 3, 3, 3, 3, 2, 2, 2, 3, 3, 3, 3, 2, 1, 4, 4, …
$ Kitchen_AbvGr <int> 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, …
$ TotRms_AbvGrd <int> 7, 5, 6, 8, 6, 7, 6, 5, 5, 7, 7, 6, 7, 5, 4, 12, 8,…
$ Functional <fct> Typ, Typ, Typ, Typ, Typ, Typ, Typ, Typ, Typ, Typ, T…
$ Fireplaces <int> 2, 0, 0, 2, 1, 1, 0, 0, 1, 1, 1, 0, 1, 1, 0, 1, 0, …
$ Garage_Type <fct> Attchd, Attchd, Attchd, Attchd, Attchd, Attchd, Att…
$ Garage_Finish <fct> Fin, Unf, Unf, Fin, Fin, Fin, Fin, RFn, RFn, Fin, F…
$ Garage_Cars <dbl> 2, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 3, 2, …
$ Garage_Area <dbl> 528, 730, 312, 522, 482, 470, 582, 506, 608, 442, 4…
$ Garage_Cond <fct> Typical, Typical, Typical, Typical, Typical, Typica…
$ Paved_Drive <fct> Partial_Pavement, Paved, Paved, Paved, Paved, Paved…
$ Wood_Deck_SF <int> 210, 140, 393, 0, 212, 360, 0, 0, 237, 140, 157, 48…
$ Open_Porch_SF <int> 62, 0, 36, 0, 34, 36, 0, 82, 152, 60, 84, 21, 75, 0…
$ Enclosed_Porch <int> 0, 0, 0, 0, 0, 0, 170, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0…
$ Three_season_porch <int> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, …
$ Screen_Porch <int> 0, 120, 0, 0, 0, 0, 0, 144, 0, 0, 0, 0, 0, 0, 140, …
$ Pool_Area <int> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, …
$ Pool_QC <fct> No_Pool, No_Pool, No_Pool, No_Pool, No_Pool, No_Poo…
$ Fence <fct> No_Fence, Minimum_Privacy, No_Fence, No_Fence, Mini…
$ Misc_Feature <fct> None, None, Gar2, None, None, None, None, None, Non…
$ Misc_Val <int> 0, 0, 12500, 0, 0, 0, 0, 0, 0, 0, 0, 500, 0, 0, 0, …
$ Mo_Sold <int> 5, 6, 6, 4, 3, 6, 4, 1, 3, 6, 4, 3, 5, 2, 6, 6, 6, …
$ Year_Sold <int> 2010, 2010, 2010, 2010, 2010, 2010, 2010, 2010, 201…
$ Sale_Type <fct> WD , WD , WD , WD , WD , WD , WD , WD , WD , WD , W…
$ Sale_Condition <fct> Normal, Normal, Normal, Normal, Normal, Normal, Nor…
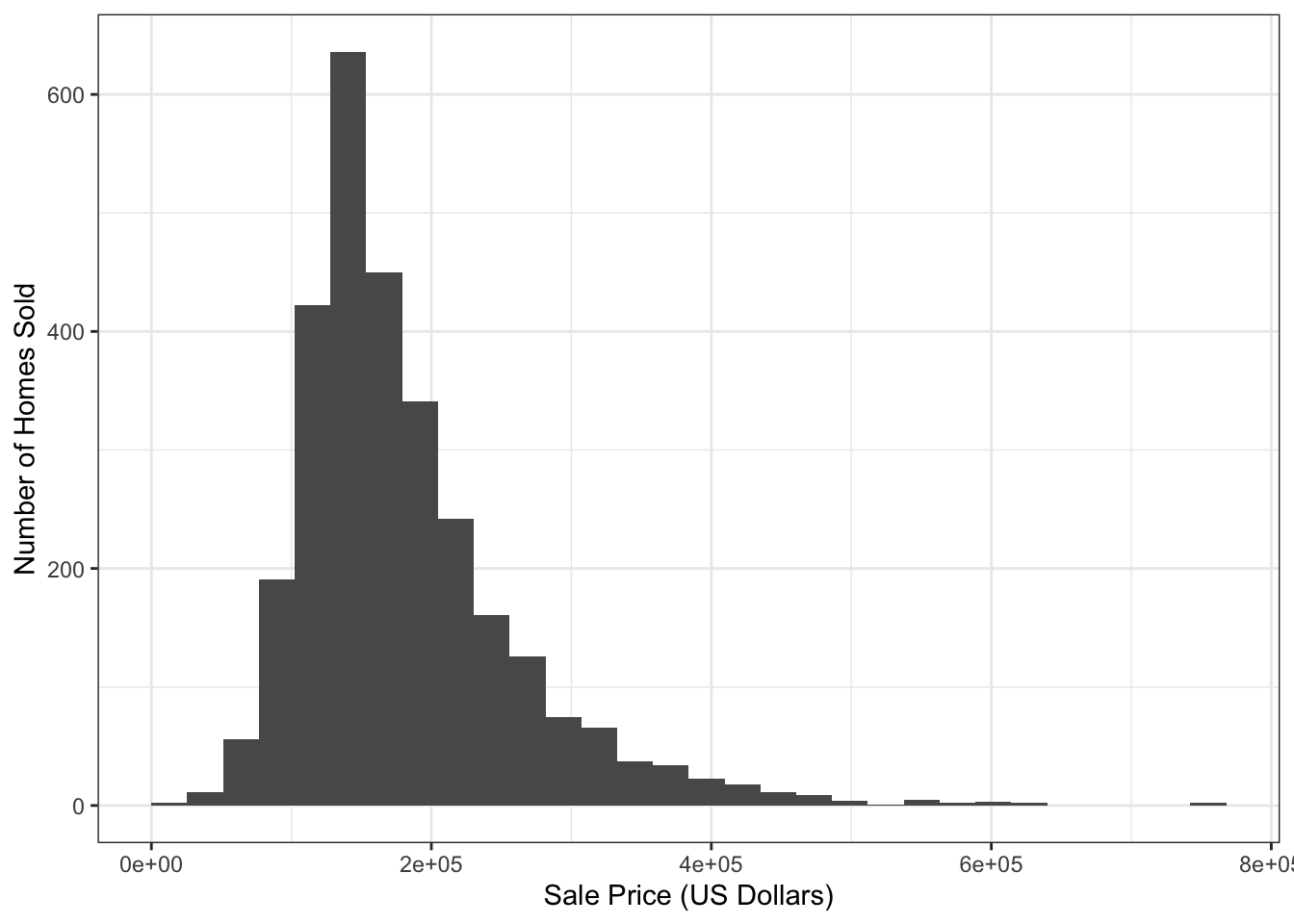
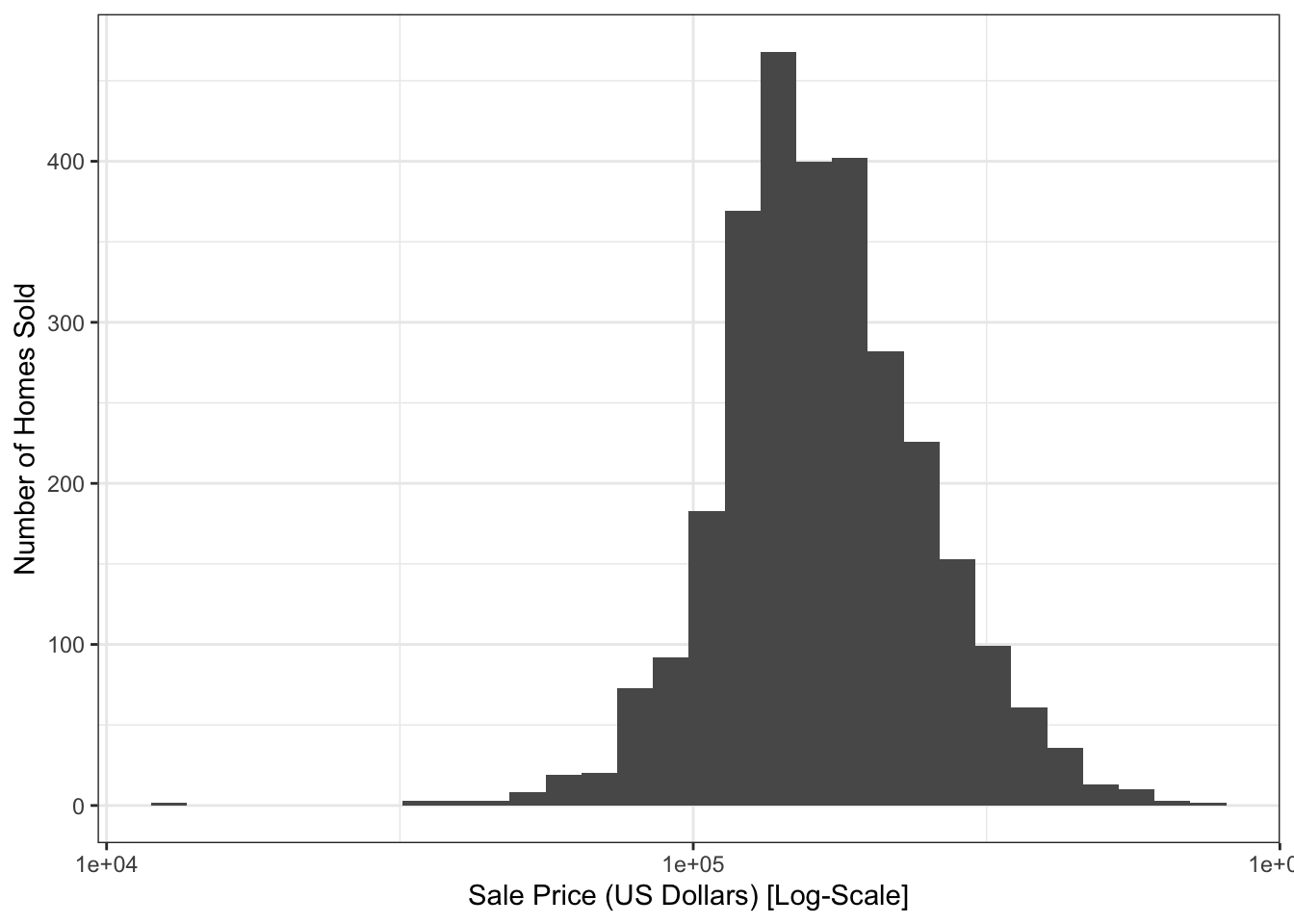
$ Sale_Price <int> 215000, 105000, 172000, 244000, 189900, 195500, 213…
$ Longitude <dbl> -93.61975, -93.61976, -93.61939, -93.61732, -93.638…
$ Latitude <dbl> 42.05403, 42.05301, 42.05266, 42.05125, 42.06090, 4…As always, we start by visualizing the data:
ggplot(ames,
aes(x=Sale_Price)) +
geom_histogram() +
theme_bw() +
xlab("Sale Price (US Dollars)") +
ylab("Number of Homes Sold")`stat_bin()` using `bins = 30`. Pick better value `binwidth`.
A quick analysis of the response variable (Sale_Price) suggests that a log-transformation might be helpful, but we won’t worry about that in this.
(Not all methods require this, and skewness in \(y\) alone does not guarantee a transformation is needed - the skewness may actually reflect a skewness in an underlying predictor, not in the unmodeled noise response - but it at least flags it as something we may want to consider.)
ggplot(ames,
aes(x=Sale_Price)) +
geom_histogram() +
theme_bw() +
scale_x_log10() +
xlab("Sale Price (US Dollars) [Log-Scale]") +
ylab("Number of Homes Sold")`stat_bin()` using `bins = 30`. Pick better value `binwidth`.
In your regression course, you might have already seen R’s built-in support for linear models via the lm function. The lm function generally takes two arguments:
formula, specifying the model to be fitdata argument, specifying the data used to fit the modelFor this data, a simple model might predict the sale price using the size of the slot on which the house sits:
lm(Sale_Price ~ Lot_Area, data=ames)
Call:
lm(formula = Sale_Price ~ Lot_Area, data = ames)
Coefficients:
(Intercept) Lot_Area
1.534e+05 2.702e+00 We see here several useful behaviors:
lm automatically dropped unused variablesIn this formula specification, as with the tests above, the left-hand side denotes the response and anything on the right-hand side is used to specify predictors. Unlike tests, it is simple to add more features to a linear model. In fact, all we need to do is to ‘add’ them to the right hand side:
lm(Sale_Price ~ Lot_Area + First_Flr_SF + Second_Flr_SF, data=ames)
Call:
lm(formula = Sale_Price ~ Lot_Area + First_Flr_SF + Second_Flr_SF,
data = ames)
Coefficients:
(Intercept) Lot_Area First_Flr_SF Second_Flr_SF
-2.136e+04 8.578e-02 1.492e+02 8.431e+01 If we add in a categorical (factor) variable, lm is also smart enough to handle this automatically for us.7
lm(Sale_Price ~ Lot_Area + First_Flr_SF + Second_Flr_SF + Central_Air, data=ames)
Call:
lm(formula = Sale_Price ~ Lot_Area + First_Flr_SF + Second_Flr_SF +
Central_Air, data = ames)
Coefficients:
(Intercept) Lot_Area First_Flr_SF Second_Flr_SF Central_AirY
-6.004e+04 9.746e-02 1.440e+02 8.288e+01 4.835e+04 Note that, unlike the numerical features we used before, you’ll see that a new variable is created Central_AirY that is a constant offset effect of having central A/C in a home.
So the formula interface lm does quite a lot of good for us! And R provides additional functionality for working with the model after we fit it:
ames_lm <- lm(Sale_Price ~ Lot_Area + First_Flr_SF + Second_Flr_SF + Central_Air,
data=ames)
predict(ames_lm) 1 2 3 4 5 6
229803.7500 118428.3170 181022.0388 293154.2649 181349.9139 178780.3095
7 8 9 10 11 12
181406.7481 173065.1833 221474.1461 201345.3606 173053.0365 159966.5755
13 14 15 16 17 18
158738.0319 182350.8856 205201.8392 368514.6157 200663.4351 256610.4910
19 20 21 22 23 24
114554.0118 288024.0187 254917.7293 158208.8760 177499.3029 133939.1792
25 26 27 28 29 30
144718.7426 141153.2402 116098.8207 113712.1539 181354.2025 99774.7213
31 32 33 34 35 36
111042.6676 111042.6676 142595.2527 161426.8588 108880.0727 161426.8588
37 38 39 40 41 42
282382.5441 234736.3151 268583.0127 211839.1804 211338.9723 233876.6310
43 44 45 46 47 48
251981.6224 210279.2031 329892.2762 184427.4205 377822.5548 279162.6406
49 50 51 52 53 54
241274.2384 186229.1424 169992.0952 180714.1869 153454.5677 171303.9220
55 56 57 58 59 60
148924.5323 204047.2492 184509.9497 154857.4241 211890.4894 292010.9580
61 62 63 64 65 66
295614.1202 236953.4698 298436.2053 248690.6206 215350.3252 383509.3403
67 68 69 70 71 72
218801.5854 164549.7886 164030.4233 214627.9279 211429.6828 200659.9048
73 74 75 76 77 78
220411.6376 177725.2523 238691.3338 121963.4856 206755.0490 121231.9759
79 80 81 82 83 84
97264.2539 195707.6921 147174.8155 172990.1652 86604.6015 227320.8173
85 86 87 88 89 90
155730.3046 117831.2486 118828.4486 138757.2468 138698.4786 204887.3158
91 92 93 94 95 96
213485.6812 260686.7429 259437.0662 202992.9007 179196.3409 124724.5603
97 98 99 100 101 102
124721.3442 124659.1648 127642.8814 201511.1690 165855.0088 160089.3100
103 104 105 106 107 108
148428.0551 110423.9684 193696.9297 201742.9923 102178.4169 165181.5438
109 110 111 112 113 114
156487.6318 203877.2127 252632.0751 274329.5207 221118.5241 225481.1218
115 116 117 118 119 120
191238.8183 188029.8749 182385.9189 166602.7914 180441.7483 165567.7623
121 122 123 124 125 126
163320.8824 206632.2776 205535.3717 155525.4972 140899.4254 238365.0984
127 128 129 130 131 132
144443.9059 311049.7264 181202.0853 112527.4412 176841.8426 142304.2466
133 134 135 136 137 138
208064.1099 171610.0286 151804.1271 245402.3295 307970.4661 261714.1544
139 140 141 142 143 144
220027.0805 202168.8573 153639.0296 234070.2157 178290.7984 161050.3346
145 146 147 148 149 150
160517.9205 171180.3667 162969.3980 216743.9872 150753.8341 142548.5931
151 152 153 154 155 156
129298.6449 131864.4134 141245.7444 130878.0757 108063.9088 145642.6823
157 158 159 160 161 162
123626.0496 166557.9197 141009.8769 174543.1673 352156.8333 140379.9767
163 164 165 166 167 168
168413.6066 159509.9601 118573.2013 149942.0776 158205.3969 190084.3396
169 170 171 172 173 174
205670.5717 212277.0242 132023.7363 123491.2627 137171.9832 182788.6662
175 176 177 178 179 180
124856.1444 96294.2600 104752.7618 122150.5553 143176.2218 187535.6726
181 182 183 184 185 186
157041.5159 60677.2433 92788.5242 127492.4772 185281.9860 247827.9064
187 188 189 190 191 192
196720.5035 166964.9137 147287.7189 255315.6334 164188.2250 185391.6114
193 194 195 196 197 198
182971.4734 50577.9553 119848.7320 139812.7718 167684.0413 153893.0266
199 200 201 202 203 204
108582.1551 172902.2593 142653.7138 186131.1138 205946.9870 166500.3657
205 206 207 208 209 210
138774.5573 58258.4443 53733.3388 202265.4061 263541.6070 230930.2761
211 212 213 214 215 216
86725.9597 130325.5127 53360.6764 154274.5273 185307.0686 72759.6340
217 218 219 220 221 222
204749.0172 195535.8782 139015.3057 189806.5348 120429.5007 141709.2101
223 224 225 226 227 228
117479.9739 141769.9146 113452.1311 186689.4894 152726.6797 145357.0858
229 230 231 232 233 234
256753.3597 203757.1068 49697.3704 142848.9111 198276.1879 222385.4491
235 236 237 238 239 240
187814.2129 61203.5706 144039.7784 153931.2289 157508.7631 157957.7073
241 242 243 244 245 246
163803.4503 207105.0256 176260.2793 123272.1819 192429.0172 195771.2910
247 248 249 250 251 252
197744.1095 215677.4994 132575.7932 233198.9338 162871.0906 165817.1767
253 254 255 256 257 258
164944.8523 360331.8074 160214.3343 140613.0589 128311.3711 183934.5827
259 260 261 262 263 264
177673.3569 137496.1051 146822.9828 118045.6602 115145.3802 274076.0191
265 266 267 268 269 270
219902.7750 198302.8589 226872.4269 228610.1360 110817.6535 110816.7764
271 272 273 274 275 276
229471.4917 202764.4933 192723.4420 32950.6971 131977.8182 180470.8562
277 278 279 280 281 282
161463.3988 82311.8743 146702.7054 149873.4807 127133.9827 150520.1856
283 284 285 286 287 288
161144.1902 58775.1821 208826.7241 127007.9346 128502.3161 65143.3244
289 290 291 292 293 294
191613.9924 112306.0805 261293.8679 181950.7649 295832.1748 240934.0497
295 296 297 298 299 300
237569.4645 255692.9716 263827.8746 181868.2855 137543.2962 160145.4733
301 302 303 304 305 306
249102.6418 133100.5433 66839.5299 125351.4759 125160.7682 139257.1254
307 308 309 310 311 312
91105.3784 126206.6319 225639.2419 211462.6720 174234.7749 213783.2526
313 314 315 316 317 318
138364.0054 284384.5001 236745.0035 183238.3311 164031.2434 154385.2890
319 320 321 322 323 324
199861.9075 196715.8522 208479.2236 280109.8595 171765.1256 195157.5422
325 326 327 328 329 330
196102.6548 182948.3586 112354.0406 124583.1404 113461.0722 112305.5056
331 332 333 334 335 336
79146.8171 112346.8286 112345.8540 114806.0930 161880.6036 109481.9402
337 338 339 340 341 342
264897.5271 133031.2793 164688.2672 248834.0721 208871.5765 116547.9155
343 344 345 346 347 348
195741.7754 335929.7217 180291.9790 240242.0271 182570.2829 241115.4852
349 350 351 352 353 354
160412.6643 352090.3997 227691.3527 201801.3068 238717.5042 149588.5721
355 356 357 358 359 360
185740.2736 182779.1258 168079.1738 152627.3482 157995.3297 160327.3186
361 362 363 364 365 366
170627.6234 154723.0069 157210.8963 215094.0929 197054.3849 184661.0612
367 368 369 370 371 372
311616.0568 284007.3011 210142.8805 207540.0005 255018.7918 218291.0555
373 374 375 376 377 378
192596.3102 220554.6985 229990.8034 229931.9362 305058.1958 201593.9212
379 380 381 382 383 384
235130.1945 352602.8729 219947.3141 186547.6411 210587.9367 207194.1293
385 386 387 388 389 390
200279.8421 208979.4886 198599.4776 222582.2406 149955.7220 161129.5546
391 392 393 394 395 396
183643.0433 249118.8555 192434.1680 133408.4810 136783.6738 158944.2162
397 398 399 400 401 402
140295.3104 113374.7480 113367.1461 113480.1995 113712.1539 113565.9642
403 404 405 406 407 408
99774.7213 148395.8922 134861.2800 99774.7213 99774.7213 134861.2800
409 410 411 412 413 414
126701.6215 165939.4646 161426.8588 140407.9503 150323.5315 161433.5835
415 416 417 418 419 420
165944.9223 160184.5207 161435.0454 108862.9197 117416.6250 150587.1258
421 422 423 424 425 426
236847.1116 329021.4520 369955.7292 335607.6859 227415.4381 220032.3818
427 428 429 430 431 432
283515.2649 295835.2198 239441.6271 280313.5801 280300.9103 285462.7619
433 434 435 436 437 438
374596.2127 329464.9188 239352.8743 246490.9256 291547.6354 236575.4763
439 440 441 442 443 444
240242.5908 235848.0747 209771.6708 249906.8861 262794.9413 253728.1141
445 446 447 448 449 450
223858.8874 242934.6819 205467.0274 333977.1330 342790.5303 256007.3157
451 452 453 454 455 456
220450.5730 184479.3666 176844.8639 176819.6218 184811.0224 177959.5325
457 458 459 460 461 462
348506.3594 306510.7071 260251.2234 198545.6293 236403.7758 179519.9143
463 464 465 466 467 468
190911.9210 169957.0096 154512.2907 158172.7432 157849.9864 160540.1160
469 470 471 472 473 474
212526.2395 214536.9447 212477.3147 205135.2062 164249.7394 153452.5210
475 476 477 478 479 480
151484.8219 238675.1542 148547.7527 177198.1311 154251.1424 173079.2743
481 482 483 484 485 486
161820.4384 142962.9936 177965.5750 236001.8595 209284.6855 222159.5235
487 488 489 490 491 492
148576.9906 199791.8342 164634.6798 154857.4241 256178.1591 184021.1264
493 494 495 496 497 498
222318.7215 154866.9752 262689.3630 312361.8004 301791.9083 272993.1156
499 500 501 502 503 504
283919.8853 261574.4225 286348.0496 292377.2518 226831.6607 248649.3015
505 506 507 508 509 510
298722.2289 204353.7246 200579.2080 233556.9333 227990.0523 216381.0173
511 512 513 514 515 516
234317.0135 195350.4447 220590.4265 347857.0525 199570.8917 168973.1942
517 518 519 520 521 522
164417.9255 195814.6074 178314.1887 190982.9249 209796.7032 243438.7352
523 524 525 526 527 528
197494.1147 218389.4449 193633.1038 217292.6459 185485.3740 253412.6367
529 530 531 532 533 534
228606.7396 218478.0927 164814.5338 212730.6807 175697.7451 164587.7980
535 536 537 538 539 540
153297.5009 155744.8704 192723.4055 206965.1324 162043.0514 149953.5484
541 542 543 544 545 546
149953.5484 149892.9284 197765.2774 221066.1655 254843.9522 195578.9201
547 548 549 550 551 552
183320.9802 128457.1961 180762.7425 162885.1459 147974.7582 203973.9335
553 554 555 556 557 558
110196.3413 53703.0899 130338.7567 130076.9797 113517.1368 113573.6635
559 560 561 562 563 564
136054.9756 120358.3550 153973.0392 113495.8906 120295.8832 279773.9540
565 566 567 568 569 570
194480.4491 321691.6964 127518.4179 127425.7336 237158.1265 169533.2751
571 572 573 574 575 576
155860.4068 160091.0643 152566.7259 192736.2418 233610.1168 165171.9927
577 578 579 580 581 582
240302.8742 287188.9224 222498.5078 169044.9027 197041.3253 203557.9875
583 584 585 586 587 588
230155.6802 239351.0247 150079.8212 285759.4242 238238.6340 181574.9342
589 590 591 592 593 594
164240.9090 259662.8212 181291.8814 231150.8040 176596.7601 113383.7143
595 596 597 598 599 600
214974.3297 122357.4477 231218.6670 179944.0004 182457.2291 117732.4243
601 602 603 604 605 606
113480.6868 113575.7101 185303.3509 238388.0015 245101.3524 207527.6320
607 608 609 610 611 612
178239.4223 175328.2800 155510.1281 216937.0234 197510.0538 139105.8754
613 614 615 616 617 618
216308.7701 127461.2528 90750.0725 148493.5889 206154.1634 232711.0057
619 620 621 622 623 624
225915.5109 140401.5416 195409.0872 149471.2050 217213.8026 198513.4232
625 626 627 628 629 630
189915.0371 215326.9245 226675.1499 239301.7850 190022.7981 211817.4990
631 632 633 634 635 636
153852.1890 201900.7158 180828.8734 131440.7555 224187.9560 164428.3094
637 638 639 640 641 642
162201.0632 188114.3873 162073.9461 189142.1985 175856.2936 257863.7770
643 644 645 646 647 648
141985.6357 179228.3382 149665.4276 134004.4920 185945.2361 103293.9184
649 650 651 652 653 654
137473.8606 163429.0776 192091.2947 164903.6739 161995.9783 129016.4988
655 656 657 658 659 660
102856.6014 163989.6950 142703.9316 119007.8728 103202.7787 144493.9028
661 662 663 664 665 666
178342.7297 185881.6611 26719.0959 154018.4617 62804.2180 93730.5472
667 668 669 670 671 672
276326.9149 187962.2230 139147.0861 289475.7677 125994.2522 148402.7324
673 674 675 676 677 678
177169.5026 202797.3462 153587.6535 138633.9986 90513.1535 81376.7862
679 680 681 682 683 684
90382.1675 216201.0690 138886.5908 181808.0049 94387.4322 159392.6731
685 686 687 688 689 690
154347.2464 161266.7380 142267.3240 199380.0785 124612.5143 139519.5539
691 692 693 694 695 696
69305.1066 140101.1908 132923.8534 155504.0586 161455.8451 123892.1311
697 698 699 700 701 702
147550.0335 157274.0983 171076.9063 221366.8859 148934.1303 210130.5864
703 704 705 706 707 708
146940.7211 109802.1154 75293.0729 145866.5144 153383.0158 112978.5296
709 710 711 712 713 714
28641.7802 57414.4393 116419.7174 103153.8538 154038.6618 165272.0379
715 716 717 718 719 720
139044.1692 183611.1036 240533.2935 222044.9983 135964.8531 190356.8292
721 722 723 724 725 726
106100.2235 162831.8116 87790.8351 206688.6549 139128.4329 162958.0838
727 728 729 730 731 732
44380.2111 55612.8120 186489.2244 146758.6148 127116.7545 187016.4490
733 734 735 736 737 738
77874.6298 144863.0895 134368.0740 154609.6345 156310.1878 133749.0677
739 740 741 742 743 744
119032.1012 176274.1629 181629.5906 179683.1574 55725.8122 114868.8719
745 746 747 748 749 750
132144.4213 180734.4960 143474.6769 206249.0585 177797.2401 199641.1730
751 752 753 754 755 756
195840.2716 228089.3177 199580.8574 183079.3130 218935.2173 110993.5685
757 758 759 760 761 762
152400.5954 154757.6717 200430.1379 117222.6800 151648.4705 90071.8880
763 764 765 766 767 768
162112.9301 162112.9301 155178.0530 71078.0482 96643.2824 75039.1381
769 770 771 772 773 774
200322.4398 150546.4998 184956.7911 140886.8235 118487.7143 137943.5637
775 776 777 778 779 780
112531.8269 112964.7730 146644.4628 170588.5245 153626.9682 287970.8736
781 782 783 784 785 786
35851.6889 205026.9627 202807.9930 166905.7497 113459.7861 258127.2256
787 788 789 790 791 792
239125.8461 188929.3611 232418.6942 143709.8622 172934.3332 179543.1558
793 794 795 796 797 798
85958.2215 145805.5819 62728.4770 139734.7067 201762.6290 136087.3376
799 800 801 802 803 804
160457.3608 142099.9413 182803.8346 257587.0994 305878.5237 197775.0939
805 806 807 808 809 810
210974.8405 226437.8826 236639.4193 209971.9123 165199.4469 241692.9789
811 812 813 814 815 816
209971.9123 209971.9123 243054.0424 165921.4056 206803.6562 291793.3025
817 818 819 820 821 822
291411.6499 291415.2559 231228.0897 236669.8322 223961.0400 236975.2033
823 824 825 826 827 828
200536.9105 188784.9732 254021.8875 248600.1242 220080.3910 174676.0493
829 830 831 832 833 834
169840.5364 166379.9983 205096.2312 150298.3468 226227.3823 193381.2711
835 836 837 838 839 840
238161.8112 139241.0374 131779.0681 192694.3970 177524.5696 200360.4344
841 842 843 844 845 846
147290.5003 131614.8483 189660.7017 205400.4476 195194.5917 192706.8034
847 848 849 850 851 852
177517.2158 215714.4159 199677.7003 195758.9668 197233.9354 204185.7705
853 854 855 856 857 858
138847.8845 120464.8048 120564.3171 138883.9446 113371.0445 171754.8539
859 860 861 862 863 864
114201.6946 117709.4238 99570.0970 99691.4345 221365.8919 235754.5434
865 866 867 868 869 870
246864.2852 223961.8246 257981.5066 183436.0914 202050.1028 207655.7474
871 872 873 874 875 876
205983.2041 252714.8037 193153.0892 222362.1065 186904.9104 163674.8033
877 878 879 880 881 882
223914.6491 110817.6535 110817.6535 219927.5445 185205.6672 205076.3789
883 884 885 886 887 888
156557.0597 142223.3441 151262.5134 203202.2149 106643.7569 178549.2760
889 890 891 892 893 894
149903.1680 154759.3213 150964.8564 234048.7450 142991.2762 89707.5921
895 896 897 898 899 900
115041.0982 186392.9428 133960.3546 113084.5127 76854.6922 230939.4816
901 902 903 904 905 906
214033.8218 127379.1916 130414.6007 148848.7080 182422.4684 144832.1326
907 908 909 910 911 912
166520.0314 3833.4466 170340.8648 315431.5613 131319.2820 234369.4968
913 914 915 916 917 918
166502.7977 193033.9674 118198.6243 219180.8369 164902.1706 129139.5135
919 920 921 922 923 924
239701.9487 170821.4651 158854.7244 157264.7836 173000.3667 128387.1801
925 926 927 928 929 930
150449.8181 270385.1510 149278.5122 171630.7275 214330.9915 127933.9386
931 932 933 934 935 936
155514.5817 264403.7263 105525.2350 124577.6028 124589.6878 124559.2804
937 938 939 940 941 942
226099.9805 330492.1562 232276.9522 141785.8353 151314.1960 75781.9477
943 944 945 946 947 948
86618.9429 23299.9044 225930.2864 58691.6620 222888.6674 260388.1209
949 950 951 952 953 954
235662.4669 201134.2740 122564.7595 174497.3612 212535.9607 164477.1663
955 956 957 958 959 960
219004.5942 183192.0081 302391.0965 222781.8235 181497.3070 282723.0230
961 962 963 964 965 966
225957.5693 200224.3273 192697.0984 258656.2168 202631.2894 175548.6956
967 968 969 970 971 972
221599.4683 254331.7123 274294.7189 134639.4870 245382.9375 162074.7848
973 974 975 976 977 978
164954.0431 102475.9372 115089.2138 79150.2282 191733.1027 79145.4527
979 980 981 982 983 984
148589.7145 112377.7233 103648.7164 146119.4320 148990.6838 109081.6728
985 986 987 988 989 990
116171.5405 151185.6484 134104.2494 214851.7104 172474.0321 192943.3114
991 992 993 994 995 996
294334.0219 231130.3738 178655.9507 152468.8785 178737.1348 182545.4339
997 998 999 1000 1001 1002
181314.8297 188927.3292 154811.1626 218117.5829 231060.9756 181309.0786
1003 1004 1005 1006 1007 1008
173071.5182 178864.2224 181667.8869 173717.5789 212755.0191 183300.1873
1009 1010 1011 1012 1013 1014
165546.5603 181363.1688 268170.9630 266197.1593 261031.9740 203548.8973
1015 1016 1017 1018 1019 1020
235272.6276 207129.5827 239274.2744 232550.0553 194198.4195 170753.1412
1021 1022 1023 1024 1025 1026
287253.0762 246255.0728 321719.0727 163917.5609 151928.5538 236728.8299
1027 1028 1029 1030 1031 1032
141641.7552 311642.5675 208667.6254 197200.8965 219172.4861 158867.7781
1033 1034 1035 1036 1037 1038
259138.4184 192434.1680 140992.0122 124057.5042 113425.6220 113929.9766
1039 1040 1041 1042 1043 1044
181178.9697 99774.7213 99774.7213 99795.1879 99793.1412 99774.7213
1045 1046 1047 1048 1049 1050
99774.7213 134861.2800 142595.2527 161429.5877 140432.2177 117643.4140
1051 1052 1053 1054 1055 1056
267654.0051 289203.7754 289766.2753 304774.7742 217292.3257 235835.2631
1057 1058 1059 1060 1061 1062
344364.0013 270437.7232 330371.1249 320450.6073 269054.5533 220133.3639
1063 1064 1065 1066 1067 1068
254079.7578 345132.9503 306786.1910 220363.3268 216103.4075 302042.8246
1069 1070 1071 1072 1073 1074
323049.8545 257924.9817 234184.3707 186301.3158 208076.0679 231600.8350
1075 1076 1077 1078 1079 1080
248240.4001 182111.2467 182111.2467 169974.5524 169974.5524 184605.4796
1081 1082 1083 1084 1085 1086
198154.8981 215574.4104 205135.2062 170872.0333 168044.2339 164408.6682
1087 1088 1089 1090 1091 1092
173831.7513 157099.9723 154229.7547 182949.6635 205461.2066 184518.0581
1093 1094 1095 1096 1097 1098
196588.4699 207487.4232 161429.4399 149438.8409 245310.8648 179283.6106
1099 1100 1101 1102 1103 1104
243700.4871 296968.9594 241805.8911 263033.0410 278232.3140 230489.2498
1105 1106 1107 1108 1109 1110
273166.3411 293515.6902 270672.1002 239048.7758 240362.5500 275753.1430
1111 1112 1113 1114 1115 1116
216929.1609 204543.8076 216067.8199 216769.9795 206534.6613 214313.5757
1117 1118 1119 1120 1121 1122
195080.1296 225412.4667 202875.9559 199468.9252 186664.0376 186664.0376
1123 1124 1125 1126 1127 1128
195018.2426 188690.8270 218636.7762 214291.4353 225720.1782 177302.9413
1129 1130 1131 1132 1133 1134
228318.8138 164382.6451 185154.7932 144515.7633 180859.7752 178384.3346
1135 1136 1137 1138 1139 1140
158735.2860 150014.2659 150014.2659 173788.4383 156492.2513 168540.0024
1141 1142 1143 1144 1145 1146
182489.9961 230810.4596 177878.3534 178634.5975 184629.7698 175290.0078
1147 1148 1149 1150 1151 1152
181757.0442 221873.7461 161685.5540 130851.2595 120862.9045 113478.2503
1153 1154 1155 1156 1157 1158
68909.5556 113308.6702 120258.6536 196073.0798 186504.1653 294887.4597
1159 1160 1161 1162 1163 1164
331882.4986 188974.6030 130473.8213 167873.4695 124721.1492 146925.7396
1165 1166 1167 1168 1169 1170
146967.0625 159170.4788 163148.7676 224580.5152 177338.5569 193015.6029
1171 1172 1173 1174 1175 1176
212855.5858 234836.3827 130397.5186 146660.3467 190879.9783 178772.7265
1177 1178 1179 1180 1181 1182
180513.2279 276753.5100 175187.3915 167753.2130 236834.1642 166750.9304
1183 1184 1185 1186 1187 1188
332371.3153 230453.5411 197366.1847 231464.0694 194822.1387 239877.2671
1189 1190 1191 1192 1193 1194
170486.1693 223024.4010 223194.8346 300563.1867 155213.6363 120463.7091
1195 1196 1197 1198 1199 1200
122262.4244 238151.8563 238349.6023 227608.5651 179631.9449 285971.5888
1201 1202 1203 1204 1205 1206
202278.7176 173322.0132 133305.2267 220276.2937 135041.9872 119716.7032
1207 1208 1209 1210 1211 1212
126183.5340 151542.9348 194443.6727 156900.7497 152743.3680 146316.4131
1213 1214 1215 1216 1217 1218
171329.2026 183533.8883 149644.4058 140873.0964 169591.3021 147881.6384
1219 1220 1221 1222 1223 1224
150359.8199 44258.1914 93656.3418 144076.0778 91540.9685 204609.0000
1225 1226 1227 1228 1229 1230
156044.0328 181718.8971 228362.8804 138189.5818 195579.3890 185376.1534
1231 1232 1233 1234 1235 1236
153765.9370 210394.5276 195207.5539 221936.4785 147096.3751 153895.4611
1237 1238 1239 1240 1241 1242
173765.8662 158468.3583 196570.4674 170730.9352 215613.1108 161361.6507
1243 1244 1245 1246 1247 1248
189861.0148 144707.1744 148255.9431 116406.4039 155063.6351 77968.7465
1249 1250 1251 1252 1253 1254
247387.2841 126073.8917 100336.3999 243116.7959 140734.7822 252105.2310
1255 1256 1257 1258 1259 1260
66049.2873 130723.6773 182512.5557 85574.2298 184974.7808 90650.4653
1261 1262 1263 1264 1265 1266
183838.1713 139594.2908 178290.8663 169754.6595 145188.8356 288858.8980
1267 1268 1269 1270 1271 1272
120177.7324 115118.0914 139879.7122 206027.8850 169901.9656 136934.4589
1273 1274 1275 1276 1277 1278
171766.7587 148519.8000 130587.1434 108786.3547 147092.4583 199921.9449
1279 1280 1281 1282 1283 1284
183169.4955 107775.9829 197890.3550 171520.7478 149851.1624 104027.6223
1285 1286 1287 1288 1289 1290
50456.6030 175392.6905 156757.1625 94680.7070 317479.8703 85515.7539
1291 1292 1293 1294 1295 1296
154032.0087 163155.4456 245170.2633 193183.9320 143522.8530 136681.0634
1297 1298 1299 1300 1301 1302
162370.9711 70040.1248 120172.7616 102476.3664 151000.7747 168638.6854
1303 1304 1305 1306 1307 1308
-735.5373 122487.2110 118600.2124 218107.4707 381912.3309 126395.3931
1309 1310 1311 1312 1313 1314
160406.4582 153593.5375 89911.7063 116793.0027 268120.6425 180730.6439
1315 1316 1317 1318 1319 1320
170522.7897 145535.9508 174061.0921 157237.0616 176208.3388 115880.0445
1321 1322 1323 1324 1325 1326
312520.9606 75235.2172 276346.1004 130914.6084 154050.5799 116518.0928
1327 1328 1329 1330 1331 1332
146486.3003 153547.5148 200266.9094 101338.8627 202912.9580 101769.2216
1333 1334 1335 1336 1337 1338
139898.3359 140749.7453 189403.7302 125510.4322 142893.6465 163355.0742
1339 1340 1341 1342 1343 1344
153501.5295 134626.5987 124137.4352 117874.5503 121180.9567 56877.5155
1345 1346 1347 1348 1349 1350
188185.2359 231467.9408 221427.4209 198357.9442 147661.1830 15436.0788
1351 1352 1353 1354 1355 1356
161128.3334 207060.3671 209242.9407 202885.6842 174280.8848 109946.4101
1357 1358 1359 1360 1361 1362
229393.3602 177762.9073 172476.6469 99481.5060 163521.5294 172095.8273
1363 1364 1365 1366 1367 1368
151471.0927 138728.0089 139561.1434 168827.2225 107876.8539 154597.8403
1369 1370 1371 1372 1373 1374
98578.5054 101711.0715 157240.7814 92620.6363 163447.9995 139700.1363
1375 1376 1377 1378 1379 1380
190000.1589 150947.7476 144159.9612 139117.8482 147356.5633 119145.3495
1381 1382 1383 1384 1385 1386
132116.5035 117959.3108 137913.2537 143749.8207 151128.3112 170667.4445
1387 1388 1389 1390 1391 1392
153679.8210 134008.6976 165924.0222 127409.6966 160714.3020 188700.2330
1393 1394 1395 1396 1397 1398
169862.1430 184709.3744 86042.0370 237091.4876 153785.2257 119441.4324
1399 1400 1401 1402 1403 1404
174442.3554 227476.0416 209679.8578 188337.3873 232902.6857 184784.4985
1405 1406 1407 1408 1409 1410
115926.8327 146818.9454 268016.5114 208745.9093 200208.6105 239853.2035
1411 1412 1413 1414 1415 1416
206477.6915 65254.2337 132324.9608 161122.0706 150714.9721 108592.2206
1417 1418 1419 1420 1421 1422
66671.0811 70551.6105 276066.0474 289246.8416 223357.1199 239275.3759
1423 1424 1425 1426 1427 1428
237689.4520 140085.5921 221715.7342 317112.3384 243691.2536 229169.0871
1429 1430 1431 1432 1433 1434
206949.1342 225956.7217 167081.7641 131778.3859 147448.4147 131729.1687
1435 1436 1437 1438 1439 1440
193291.7893 189631.3797 173867.2948 191430.7047 185813.5416 202140.3843
1441 1442 1443 1444 1445 1446
204633.2380 196861.4294 197269.1919 193622.1320 124238.7116 130925.5386
1447 1448 1449 1450 1451 1452
158511.2111 137079.9516 144107.1527 213995.6855 122105.3044 113388.5873
1453 1454 1455 1456 1457 1458
101297.6519 247667.7498 226459.8290 204476.6012 247219.9734 204010.3060
1459 1460 1461 1462 1463 1464
228175.0713 241206.5384 234059.3872 246870.8830 249381.9182 189629.9797
1465 1466 1467 1468 1469 1470
251193.2542 173677.3341 189764.8475 204284.0311 110817.6535 110816.7764
1471 1472 1473 1474 1475 1476
204520.6572 253895.5796 210322.1977 183141.0460 197281.5105 195859.1466
1477 1478 1479 1480 1481 1482
167266.5631 167031.9365 214540.5744 185176.6384 154246.3228 110816.7764
1483 1484 1485 1486 1487 1488
110816.7764 110817.9459 110817.9459 103754.7527 249194.6817 146469.9123
1489 1490 1491 1492 1493 1494
170090.7453 138198.0165 151184.5603 133047.3038 159300.8364 172653.5677
1495 1496 1497 1498 1499 1500
150050.7601 146654.2581 151955.4438 542824.4855 748742.2314 142991.2762
1501 1502 1503 1504 1505 1506
106392.9602 106390.2313 148445.6648 106471.4153 53501.4455 112498.5498
1507 1508 1509 1510 1511 1512
140070.2180 123118.1954 135819.7951 171835.0554 158626.3120 162385.8766
1513 1514 1515 1516 1517 1518
153855.0003 64889.1492 65146.8330 139909.7608 113449.6543 200246.8474
1519 1520 1521 1522 1523 1524
214427.8086 194018.5382 166116.0506 265308.6695 206835.6174 139297.4385
1525 1526 1527 1528 1529 1530
256282.4154 180371.8038 135874.7007 54302.9462 163105.8911 157187.0039
1531 1532 1533 1534 1535 1536
172129.6989 165474.5603 178914.2347 227337.1571 160014.1909 97782.8493
1537 1538 1539 1540 1541 1542
204526.9533 395579.0866 221230.7117 243016.2169 264087.5460 225844.3062
1543 1544 1545 1546 1547 1548
105539.4641 161192.4153 121289.0047 125652.1773 54907.8703 106352.6444
1549 1550 1551 1552 1553 1554
100980.4882 136200.7529 192842.0217 120319.4685 221519.6569 46905.1970
1555 1556 1557 1558 1559 1560
103667.2435 89583.8859 68389.0848 118761.9899 87178.5855 226676.1080
1561 1562 1563 1564 1565 1566
225930.2864 225639.2419 225642.2631 283150.2278 232751.0322 195809.7756
1567 1568 1569 1570 1571 1572
150218.3083 173420.2147 201630.7245 232431.8513 251269.6873 204791.2262
1573 1574 1575 1576 1577 1578
407019.8198 210702.7930 226195.6400 193280.9765 152264.9064 150845.5274
1579 1580 1581 1582 1583 1584
171701.5293 204785.6799 227197.6981 170902.3906 206538.9938 196703.2076
1585 1586 1587 1588 1589 1590
230214.1414 267498.3958 238188.5987 272163.6508 182662.3140 182479.0896
1591 1592 1593 1594 1595 1596
146416.6018 159915.3412 162438.1535 138437.9685 134267.8935 167314.8528
1597 1598 1599 1600 1601 1602
102512.7770 102475.9372 157054.0776 112305.6031 79185.7036 132659.9779
1603 1604 1605 1606 1607 1608
106411.1203 121860.0808 106421.8409 106421.8409 110596.7653 194609.1792
1609 1610 1611 1612 1613 1614
117495.9130 223837.7314 216234.8214 217813.6146 173181.3111 309664.8463
1615 1616 1617 1618 1619 1620
309016.8449 184881.9538 168835.9090 159990.6593 177720.5274 149932.6094
1621 1622 1623 1624 1625 1626
226651.0608 186133.9079 189049.2474 159994.1743 169457.8944 238034.6492
1627 1628 1629 1630 1631 1632
160120.1722 160344.4129 161622.3562 180726.0786 152464.9047 145296.7294
1633 1634 1635 1636 1637 1638
234706.9912 158499.1024 178978.6756 266381.3247 271206.3434 329955.5337
1639 1640 1641 1642 1643 1644
197362.3846 221156.1731 193376.5941 311290.4435 283628.9031 196834.1936
1645 1646 1647 1648 1649 1650
174221.4082 213938.2585 156348.5567 229057.8132 215644.1849 223578.5114
1651 1652 1653 1654 1655 1656
226016.8932 137887.6897 158904.1159 195928.7689 184100.2716 171267.8788
1657 1658 1659 1660 1661 1662
165206.6973 203139.0314 197493.0145 219642.1035 179788.0263 210864.9908
1663 1664 1665 1666 1667 1668
116426.4171 130558.7383 155898.4872 193941.8078 120658.8531 126020.6491
1669 1670 1671 1672 1673 1674
114648.8608 112540.4034 121563.1828 113565.9642 99119.9153 181184.1351
1675 1676 1677 1678 1679 1680
181849.7857 111093.8340 130485.1808 130501.5541 134894.0265 148352.2302
1681 1682 1683 1684 1685 1686
126701.6215 165939.4646 140410.2893 131237.0645 250956.7439 252608.7675
1687 1688 1689 1690 1691 1692
233350.4838 233330.5046 239114.3606 295191.0599 295058.4998 328448.4212
1693 1694 1695 1696 1697 1698
271083.3375 284356.8895 235120.5937 357052.0345 273730.1579 335072.3547
1699 1700 1701 1702 1703 1704
224654.0383 274235.2389 323404.4531 319653.2250 264919.9586 264020.9670
1705 1706 1707 1708 1709 1710
221817.6975 266781.9683 249052.9521 339513.5527 263423.4178 261704.1945
1711 1712 1713 1714 1715 1716
261608.8820 194875.7292 221628.3955 236966.9340 220141.6068 185120.8087
1717 1718 1719 1720 1721 1722
176124.7717 176124.9666 184995.2805 212470.5752 212470.5752 186161.8951
1723 1724 1725 1726 1727 1728
216098.5640 213743.6987 258133.6875 179519.9143 190888.7256 160746.6060
1729 1730 1731 1732 1733 1734
163518.7030 160125.1186 147570.0438 158153.6300 176598.4742 180390.2600
1735 1736 1737 1738 1739 1740
154326.1424 176621.0371 182082.4665 143787.6238 159693.5009 154198.9573
1741 1742 1743 1744 1745 1746
170160.3611 169792.4503 190523.1095 217414.8385 170923.4921 209988.3092
1747 1748 1749 1750 1751 1752
150980.0690 148708.5614 203554.7825 208914.1308 182972.4691 151061.4009
1753 1754 1755 1756 1757 1758
202260.9514 187065.2430 207279.0541 183792.5397 155073.4925 138777.1763
1759 1760 1761 1762 1763 1764
186715.3706 184201.3522 508071.3632 309587.1670 239658.7001 368470.2579
1765 1766 1767 1768 1769 1770
346509.3686 289562.4614 254706.4255 497402.2856 224950.4534 272678.5673
1771 1772 1773 1774 1775 1776
272288.1773 280388.0444 454254.1083 239450.6848 281082.6463 186355.9228
1777 1778 1779 1780 1781 1782
211448.6294 263691.5726 200553.4196 210178.2200 272533.8327 225143.9984
1783 1784 1785 1786 1787 1788
247691.5300 209251.3860 237702.5370 232418.1094 217892.5718 210582.0551
1789 1790 1791 1792 1793 1794
204565.9228 205917.1559 233160.8270 213079.1622 220361.2599 181769.2986
1795 1796 1797 1798 1799 1800
181372.4954 192399.0825 165218.9524 218003.0216 277822.4251 203645.0575
1801 1802 1803 1804 1805 1806
227788.8657 188638.6888 217359.6025 232034.7409 262551.5383 290284.8456
1807 1808 1809 1810 1811 1812
147395.0215 153585.4267 147013.6701 202958.9552 188940.4582 196475.4644
1813 1814 1815 1816 1817 1818
183334.3733 204963.9192 215827.3038 132494.6790 116462.7652 279928.6138
1819 1820 1821 1822 1823 1824
117620.2481 128775.3537 141196.8195 132879.9121 150222.6260 233798.5361
1825 1826 1827 1828 1829 1830
138754.9078 131509.4647 118761.0359 275293.7535 262217.8258 138642.2000
1831 1832 1833 1834 1835 1836
234808.1962 141424.6511 310885.4052 357423.1798 187112.5388 154349.5323
1837 1838 1839 1840 1841 1842
213975.6146 183354.9816 183294.1666 211966.8438 167379.3866 130496.6269
1843 1844 1845 1846 1847 1848
159170.4788 153988.8889 160005.2022 165855.0088 161876.7200 113793.4069
1849 1850 1851 1852 1853 1854
154660.7640 210198.8051 184520.0073 224305.6365 259409.6724 204308.0146
1855 1856 1857 1858 1859 1860
329514.7848 196034.4177 196229.0213 175111.0863 209808.3631 170921.6788
1861 1862 1863 1864 1865 1866
349512.9007 290426.6083 213433.0057 155290.4241 274608.5781 144922.8825
1867 1868 1869 1870 1871 1872
175877.1205 221192.1063 218712.2000 227949.5787 231283.3494 146702.8560
1873 1874 1875 1876 1877 1878
168042.4205 140806.4192 148456.3648 164085.0412 143779.8383 182717.1839
1879 1880 1881 1882 1883 1884
238108.1943 117231.8471 194222.9794 127466.0963 142491.9837 153156.2373
1885 1886 1887 1888 1889 1890
120333.4053 143647.1128 116092.8756 160588.0768 127888.4782 117853.6644
1891 1892 1893 1894 1895 1896
161918.0104 139210.8543 176655.8303 219302.4273 187219.1982 228275.9109
1897 1898 1899 1900 1901 1902
195449.3222 180063.6869 165474.6734 123285.2711 120209.4748 -11470.0595
1903 1904 1905 1906 1907 1908
36325.6271 22828.6169 105131.2573 221925.8037 154797.8327 205226.1020
1909 1910 1911 1912 1913 1914
162401.5119 179725.9031 213731.7938 173556.8681 169769.9755 120588.2627
1915 1916 1917 1918 1919 1920
169106.6997 276844.7992 123907.9034 134088.0594 140701.8595 141126.5363
1921 1922 1923 1924 1925 1926
196849.6218 141231.2081 168563.0804 153885.3253 237013.9096 121990.8571
1927 1928 1929 1930 1931 1932
140167.4136 228036.0386 192625.3532 164343.2418 155564.3158 213674.2925
1933 1934 1935 1936 1937 1938
125848.8954 138800.3241 134289.1190 122302.8702 184789.7082 180163.6441
1939 1940 1941 1942 1943 1944
122289.2259 123198.6677 226340.7724 122864.8088 178738.0095 117799.3645
1945 1946 1947 1948 1949 1950
164542.9369 326044.8479 119886.6919 115816.1872 147091.9304 128713.5346
1951 1952 1953 1954 1955 1956
162369.4187 88309.5252 189344.5593 116991.8361 126166.4785 225353.6739
1957 1958 1959 1960 1961 1962
106719.8789 145209.5118 213669.8182 131241.9375 167232.6653 113390.5365
1963 1964 1965 1966 1967 1968
152241.0306 138757.2468 157454.3952 167877.0312 187321.4779 199871.9480
1969 1970 1971 1972 1973 1974
122152.7821 204972.3724 192732.7321 113332.0606 123712.9838 127189.3399
1975 1976 1977 1978 1979 1980
154836.9954 149200.3476 87525.7444 123755.8661 127824.2965 140086.6046
1981 1982 1983 1984 1985 1986
143334.8221 128020.0106 128412.4784 151704.3726 81587.0402 127094.0242
1987 1988 1989 1990 1991 1992
208875.0236 113354.8957 128491.3262 143355.0747 181185.5975 162672.2963
1993 1994 1995 1996 1997 1998
128486.2187 221835.8725 186409.1729 244391.2411 143171.4078 273150.0383
1999 2000 2001 2002 2003 2004
207504.3359 192949.9732 213532.4737 297300.6187 148366.9903 128501.6570
2005 2006 2007 2008 2009 2010
188411.6397 84431.9118 163669.0198 157160.5096 180556.7725 138959.8462
2011 2012 2013 2014 2015 2016
128136.8336 142918.8740 116164.5381 158283.8833 153394.3469 169038.3905
2017 2018 2019 2020 2021 2022
150228.8576 171656.2016 111845.6508 160788.9063 82508.7613 243893.3768
2023 2024 2025 2026 2027 2028
205543.8224 149145.2533 156848.1886 147492.7562 92953.6694 251787.1073
2029 2030 2031 2032 2033 2034
94721.4410 100318.5109 214625.0547 148541.7544 271159.9883 148495.6709
2035 2036 2037 2038 2039 2040
150787.2843 210657.7009 239502.4679 148902.0359 68230.1299 160952.3195
2041 2042 2043 2044 2045 2046
112453.6051 156390.5091 109661.3696 155754.5692 254537.5481 306062.8608
2047 2048 2049 2050 2051 2052
80919.2863 94171.2161 133218.7799 198433.9787 134381.1742 137216.8295
2053 2054 2055 2056 2057 2058
136525.9989 139164.3365 120561.6709 117699.0931 125656.7046 114085.7764
2059 2060 2061 2062 2063 2064
118284.0912 124880.3634 126543.9846 117857.9526 174096.0896 120395.1948
2065 2066 2067 2068 2069 2070
187635.3664 305621.6956 194625.8872 145637.6262 176421.2977 158947.2758
2071 2072 2073 2074 2075 2076
84511.1529 262115.6213 208495.7890 231116.5144 180765.2706 225175.9741
2077 2078 2079 2080 2081 2082
120496.5294 338217.9551 300206.2887 184442.8129 113215.1088 76838.3042
2083 2084 2085 2086 2087 2088
196362.9754 76289.1212 138115.4444 182407.5245 129673.1838 113805.5434
2089 2090 2091 2092 2093 2094
182098.1576 209140.8150 196908.7799 244054.0499 310441.8609 221578.6405
2095 2096 2097 2098 2099 2100
225446.3004 214347.2035 291030.2670 313209.6298 226882.1233 297406.9771
2101 2102 2103 2104 2105 2106
204423.6019 178849.1752 226985.1383 293098.4196 172572.6303 154529.3461
2107 2108 2109 2110 2111 2112
167652.7467 162871.0906 212016.6842 205102.9854 171843.5718 191675.2161
2113 2114 2115 2116 2117 2118
178380.1690 232682.0751 202190.2223 269700.1369 221254.6586 222082.9781
2119 2120 2121 2122 2123 2124
241187.6587 136820.5520 131683.3625 162156.6895 137148.7888 191962.2967
2125 2126 2127 2128 2129 2130
131649.5440 147846.2162 131614.6534 192519.4629 204944.4415 186901.9722
2131 2132 2133 2134 2135 2136
180918.0484 201997.5495 202265.4252 178962.1502 118157.7390 136710.8566
2137 2138 2139 2140 2141 2142
134510.7574 138901.6823 120467.8260 115791.1932 116030.5988 128814.2254
2143 2144 2145 2146 2147 2148
113390.5365 114974.1285 277242.9108 247416.6339 230261.3799 199199.4340
2149 2150 2151 2152 2153 2154
209876.9098 184931.6546 267019.5985 218656.2285 285208.5191 228925.7596
2155 2156 2157 2158 2159 2160
229531.2346 237020.7047 110817.6535 183038.0748 200635.0055 181606.8183
2161 2162 2163 2164 2165 2166
156509.4993 195498.9722 193848.5388 160475.3600 180587.7726 157771.0370
2167 2168 2169 2170 2171 2172
163402.5309 163969.5513 124011.6981 145746.2141 127573.6240 156899.2389
2173 2174 2175 2176 2177 2178
158840.2118 106932.6278 139214.6848 149307.1801 241499.4930 151095.0627
2179 2180 2181 2182 2183 2184
145909.0015 150519.9127 725625.1000 571439.0434 142991.2762 127133.0081
2185 2186 2187 2188 2189 2190
106475.0214 125777.2624 112846.6043 100148.3172 106176.2433 117928.7084
2191 2192 2193 2194 2195 2196
101284.8751 99664.8279 113485.2674 125579.9063 316022.0485 235010.0968
2197 2198 2199 2200 2201 2202
168798.1569 54578.2554 193724.0826 142910.3614 195461.5570 114331.5001
2203 2204 2205 2206 2207 2208
111611.7911 162944.6759 151993.5403 181494.8965 40286.4175 132803.8530
2209 2210 2211 2212 2213 2214
126259.9720 162734.7075 167640.8737 184357.0940 166080.9030 243306.0612
2215 2216 2217 2218 2219 2220
372711.6040 209652.9461 221365.5903 147637.1853 309967.4076 269009.8904
2221 2222 2223 2224 2225 2226
254460.1791 192435.6182 315563.7433 215370.7756 204624.7679 107401.5283
2227 2228 2229 2230 2231 2232
231904.2659 135527.8155 234482.7041 353555.4098 382506.3317 127416.5886
2233 2234 2235 2236 2237 2238
133666.4884 56048.5459 178880.3185 129126.0812 198233.4993 106136.4785
2239 2240 2241 2242 2243 2244
134800.6472 144226.8481 174354.1924 81519.7215 168937.8555 143416.8980
2245 2246 2247 2248 2249 2250
133002.3512 222787.2576 222707.5355 176496.8290 120333.8926 144680.1780
2251 2252 2253 2254 2255 2256
189675.8412 192402.3356 202049.6345 121315.5964 136830.4545 204788.3024
2257 2258 2259 2260 2261 2262
205488.6635 181135.1749 318341.4484 232273.7714 214271.5853 202826.5752
2263 2264 2265 2266 2267 2268
215541.7850 226306.3543 167825.7379 204456.6370 188991.3266 177838.9451
2269 2270 2271 2272 2273 2274
154221.0065 266103.3693 203711.5162 224237.1289 265496.9546 218038.6228
2275 2276 2277 2278 2279 2280
245474.7209 252124.4306 264455.6686 150362.1885 285364.9342 123708.1108
2281 2282 2283 2284 2285 2286
140490.6672 225688.8372 224976.5507 141317.2267 153122.1854 112308.2345
2287 2288 2289 2290 2291 2292
103045.6489 112307.3574 112356.6720 79190.1867 112345.8540 142297.9944
2293 2294 2295 2296 2297 2298
134309.1957 185073.7445 232898.6868 151532.6747 103554.5702 99574.3852
2299 2300 2301 2302 2303 2304
174150.7351 110694.1276 158965.2380 106588.8870 106911.5764 129568.7356
2305 2306 2307 2308 2309 2310
117018.1355 175523.6042 136749.4359 248152.8369 192251.6747 255923.1306
2311 2312 2313 2314 2315 2316
165160.8750 235548.7071 175774.9822 155938.2212 186603.2406 163617.9981
2317 2318 2319 2320 2321 2322
279272.5069 230171.0878 226252.6959 193628.0903 276817.0700 212253.6683
2323 2324 2325 2326 2327 2328
339272.9244 157384.5993 156032.3355 182785.2238 161996.9144 200263.8844
2329 2330 2331 2332 2333 2334
239727.8908 308137.3524 364364.9707 261779.8482 349247.5750 280226.0890
2335 2336 2337 2338 2339 2340
326483.7833 306412.9004 320825.6911 272128.5279 95360.8461 235851.3056
2341 2342 2343 2344 2345 2346
252282.6374 278010.4068 223047.3188 254692.4500 267156.4154 168846.5318
2347 2348 2349 2350 2351 2352
147971.8182 258817.0226 200963.5604 232024.3275 305698.4171 167591.9760
2353 2354 2355 2356 2357 2358
145184.1870 239988.7233 212472.8495 143909.2797 178027.2608 177740.5639
2359 2360 2361 2362 2363 2364
148070.5598 147634.9086 113600.3675 112616.9094 114830.1656 193443.2566
2365 2366 2367 2368 2369 2370
111147.9242 148375.6206 99801.3278 104030.9724 130464.7143 130464.7143
2371 2372 2373 2374 2375 2376
96542.3617 111042.6676 99774.7213 142595.2527 188713.7415 118635.3807
2377 2378 2379 2380 2381 2382
140407.9503 161417.0154 274982.6199 310641.2293 281339.8749 222812.1040
2383 2384 2385 2386 2387 2388
288525.6887 239992.0748 258668.0449 256198.8297 257348.3910 261981.5435
2389 2390 2391 2392 2393 2394
240730.8702 226590.2383 261836.1005 254281.2632 250137.8268 251728.0270
2395 2396 2397 2398 2399 2400
279183.4775 269375.1277 221070.5879 247627.2597 246003.9868 247440.9165
2401 2402 2403 2404 2405 2406
329274.8265 211799.9139 235329.8495 185357.5681 214182.9116 185923.9662
2407 2408 2409 2410 2411 2412
185908.0802 231780.6779 228768.1921 190878.3948 178757.7579 154444.9459
2413 2414 2415 2416 2417 2418
158039.4815 154520.2019 197772.8899 180336.0723 154965.4788 250373.2309
2419 2420 2421 2422 2423 2424
157926.0382 184971.1399 212766.6050 198226.3509 206119.1664 192167.8236
2425 2426 2427 2428 2429 2430
211458.8537 168263.9378 153003.8692 205406.6613 214282.8375 204643.4624
2431 2432 2433 2434 2435 2436
187611.5832 163431.5450 149566.1234 173439.9855 238666.5586 163432.9094
2437 2438 2439 2440 2441 2442
185221.3987 207281.4676 204105.6733 186434.2200 248024.8544 240424.1872
2443 2444 2445 2446 2447 2448
273419.6780 218926.5853 247994.9984 404240.4296 319896.1369 215273.4737
2449 2450 2451 2452 2453 2454
248203.3073 298164.1843 398140.1329 275719.5969 272130.1308 317108.5327
2455 2456 2457 2458 2459 2460
220463.6637 230206.0759 292231.6159 228275.6391 221795.6660 205890.9096
2461 2462 2463 2464 2465 2466
173131.5239 332756.2579 203758.7547 216941.3851 163988.8624 183728.8214
2467 2468 2469 2470 2471 2472
167238.9275 170687.7752 171292.8648 176302.3288 153464.1719 190927.3433
2473 2474 2475 2476 2477 2478
152400.9179 153840.5470 156287.9165 183226.4190 171174.1494 198844.6670
2479 2480 2481 2482 2483 2484
171336.6046 184238.2276 190264.2947 164207.0077 137434.8873 141197.0972
2485 2486 2487 2488 2489 2490
127989.2664 131427.1112 237959.6656 204811.4122 163544.4848 163613.5011
2491 2492 2493 2494 2495 2496
130871.5312 119990.6923 122312.4213 136994.9372 124228.4340 72034.8319
2497 2498 2499 2500 2501 2502
166924.5653 124630.5443 340391.7950 269660.9396 316445.5975 281164.9169
2503 2504 2505 2506 2507 2508
251038.9912 223315.0852 153208.0623 168149.7976 113204.1163 115048.3953
2509 2510 2511 2512 2513 2514
115048.3953 113204.1163 161818.6192 152563.5097 144212.9163 110623.1762
2515 2516 2517 2518 2519 2520
181679.5314 214738.4769 204316.1038 163308.4903 166465.5148 137805.2003
2521 2522 2523 2524 2525 2526
165180.9590 165181.1540 258383.9556 161330.3219 223071.8080 300714.2198
2527 2528 2529 2530 2531 2532
150050.6511 301701.7974 199490.3495 181339.6367 156813.3135 130338.7567
2533 2534 2535 2536 2537 2538
140545.5045 189842.7174 129724.8958 140572.5156 118402.2273 140561.0006
2539 2540 2541 2542 2543 2544
153502.1665 161959.9181 221936.2725 140504.7515 113575.7101 235587.3549
2545 2546 2547 2548 2549 2550
214464.4731 169260.1189 203532.1459 152543.7477 146956.0862 140772.3230
2551 2552 2553 2554 2555 2556
169023.1498 106611.8875 134532.9635 139405.8862 137985.1379 113983.6533
2557 2558 2559 2560 2561 2562
96412.8686 149969.4627 195539.3366 223158.8571 164299.3849 248504.6785
2563 2564 2565 2566 2567 2568
178532.4633 194993.2919 124017.8381 217211.1712 168920.3976 166927.4744
2569 2570 2571 2572 2573 2574
242738.7364 151572.1728 299289.9432 134367.0868 160373.9044 153794.0055
2575 2576 2577 2578 2579 2580
185488.9440 188536.1107 181575.9088 186508.6571 146959.6479 151108.5948
2581 2582 2583 2584 2585 2586
167218.6991 124747.2332 140254.5722 187356.1440 134664.8266 216037.6221
2587 2588 2589 2590 2591 2592
153892.8445 134064.5273 141655.1583 117071.6941 283921.0433 188845.7553
2593 2594 2595 2596 2597 2598
294294.1220 152749.4180 150397.0597 91964.9829 108752.2586 143303.3573
2599 2600 2601 2602 2603 2604
43956.1871 76026.8895 152035.5263 168479.1889 195151.1185 132327.8161
2605 2606 2607 2608 2609 2610
248956.9951 177806.7633 179755.5721 145954.5537 154278.8976 199248.1506
2611 2612 2613 2614 2615 2616
162994.9473 120359.2321 161064.9535 113403.4012 106470.5708 244603.6783
2617 2618 2619 2620 2621 2622
201353.6828 309034.2771 220236.1703 171134.9728 83784.7309 138728.0089
2623 2624 2625 2626 2627 2628
138728.0089 138763.0944 90513.1535 90513.1535 90513.1535 213140.7384
2629 2630 2631 2632 2633 2634
154636.5367 154544.4372 141082.2512 133118.3963 139467.3154 113371.0445
2635 2636 2637 2638 2639 2640
136549.0733 217697.2696 100466.7906 202372.4232 147891.7849 164016.9851
2641 2642 2643 2644 2645 2646
176068.3691 159085.1220 54220.6216 105900.6789 168627.4924 89283.1900
2647 2648 2649 2650 2651 2652
110358.5587 200741.9710 113390.5365 126228.7808 146703.6810 127094.0242
2653 2654 2655 2656 2657 2658
168524.1272 59897.7332 141260.9840 156300.9524 109793.8175 156106.9669
2659 2660 2661 2662 2663 2664
154810.2413 141297.2996 238186.9289 114096.7963 179018.0519 95471.1309
2665 2666 2667 2668 2669 2670
196002.6631 162165.5584 334890.6555 82092.0598 127459.4985 87265.2048
2671 2672 2673 2674 2675 2676
102473.3303 179006.9891 154646.8190 188032.4033 130163.9760 106386.7553
2677 2678 2679 2680 2681 2682
155034.4836 129676.6850 86677.8381 57201.6986 183180.8360 143897.4743
2683 2684 2685 2686 2687 2688
147680.7205 77570.7827 139799.7951 106916.1571 295977.8791 79125.6447
2689 2690 2691 2692 2693 2694
185475.8207 40126.6661 158772.8095 139888.7852 58741.7918 150831.1814
2695 2696 2697 2698 2699 2700
150773.5250 95960.8263 15480.5205 130666.0859 173397.2694 265942.9356
2701 2702 2703 2704 2705 2706
226486.7613 183618.1231 89332.7970 115357.0097 143313.1033 188356.5749
2707 2708 2709 2710 2711 2712
175932.4924 142877.2866 142585.3354 179483.6977 123776.4981 141638.7319
2713 2714 2715 2716 2717 2718
156283.8379 146149.8015 199132.0745 237072.2881 138725.6699 272421.5738
2719 2720 2721 2722 2723 2724
269691.1662 225241.2809 249149.1597 246161.3696 67203.0609 127507.8386
2725 2726 2727 2728 2729 2730
196561.0669 253740.7928 133539.6324 259024.2368 105969.3438 118308.8017
2731 2732 2733 2734 2735 2736
171517.0052 197996.6913 183568.4865 84708.9512 223413.2051 268848.9558
2737 2738 2739 2740 2741 2742
238423.6492 406720.0261 214025.2453 203695.8784 141498.8475 217253.0448
2743 2744 2745 2746 2747 2748
187824.1943 154199.9847 150931.5103 170922.9217 176260.2793 281779.9121
2749 2750 2751 2752 2753 2754
212673.8419 196495.3258 224757.1261 162941.8464 164661.4097 175251.9010
2755 2756 2757 2758 2759 2760
221753.5339 204837.4754 236736.0884 255364.1247 239071.4783 218340.8190
2761 2762 2763 2764 2765 2766
197029.5184 221568.9450 169379.1138 204623.5274 219611.4795 132631.0323
2767 2768 2769 2770 2771 2772
215896.3677 189294.9092 120749.1009 147932.5124 162315.8257 194298.4576
2773 2774 2775 2776 2777 2778
132150.4874 208735.1946 204285.5988 217918.3012 186453.5176 195147.5762
2779 2780 2781 2782 2783 2784
200052.6198 194039.2314 211487.3061 126696.1047 146058.7160 173877.4430
2785 2786 2787 2788 2789 2790
129059.6587 113620.5417 117962.8194 113390.5365 136541.4307 220903.3851
2791 2792 2793 2794 2795 2796
188938.9010 185992.5955 184887.1385 247007.1466 200638.5774 227211.3868
2797 2798 2799 2800 2801 2802
239412.4666 225278.8934 215465.2117 212776.7212 230735.3346 253507.6600
2803 2804 2805 2806 2807 2808
110817.6535 110817.6535 214782.3507 189271.9382 202701.2749 233932.1151
2809 2810 2811 2812 2813 2814
185086.1912 170533.0559 212718.0936 184525.5678 181494.2375 159299.9457
2815 2816 2817 2818 2819 2820
154271.8573 177750.7145 154599.6549 201084.8975 164804.7731 134759.4217
2821 2822 2823 2824 2825 2826
130304.6458 159177.5734 181121.7572 120671.5229 252268.7736 142991.2762
2827 2828 2829 2830 2831 2832
142991.2762 142991.2762 189443.7592 189443.7592 189443.7592 189443.7592
2833 2834 2835 2836 2837 2838
189809.3332 104674.5347 151637.2841 145898.5392 127447.5177 148418.3734
2839 2840 2841 2842 2843 2844
113485.2674 203218.4316 134612.1694 79543.1241 143794.6952 12440.8139
2845 2846 2847 2848 2849 2850
111017.8345 206695.3168 194128.3728 182539.3091 101489.0839 156951.9603
2851 2852 2853 2854 2855 2856
191929.4963 160049.4915 134004.2439 174779.2281 193430.7744 171309.3808
2857 2858 2859 2860 2861 2862
97644.6333 190242.0178 176310.1019 163526.6861 200537.2091 159311.6397
2863 2864 2865 2866 2867 2868
222215.4419 196129.1816 255740.6055 181438.6680 206392.8970 250397.3482
2869 2870 2871 2872 2873 2874
226677.2037 259757.4582 182174.3121 255368.9682 81177.1176 148080.7067
2875 2876 2877 2878 2879 2880
37533.8275 81270.2391 77721.9930 184013.1536 154900.3245 46113.1795
2881 2882 2883 2884 2885 2886
9938.3648 121284.8749 53549.1895 244831.1258 225642.2631 224542.7039
2887 2888 2889 2890 2891 2892
228676.3555 203842.0149 133869.8853 163579.8479 271407.0939 275252.8397
2893 2894 2895 2896 2897 2898
175539.8120 230726.6059 235674.1178 153336.7182 181855.6628 277040.6714
2899 2900 2901 2902 2903 2904
191074.0646 248834.8075 271799.3845 281376.8873 254036.9938 221691.1479
2905 2906 2907 2908 2909 2910
185930.3010 163802.3398 181221.8521 154100.5550 134267.8935 167314.8528
2911 2912 2913 2914 2915 2916
276490.9698 115119.8162 227285.1344 79144.7705 112306.2853 185398.8320
2917 2918 2919 2920 2921 2922
79150.9104 112311.0608 112310.3786 112350.3371 112346.2438 238304.6733
2923 2924 2925 2926 2927 2928
237978.8651 152102.9094 166464.6703 133473.2091 119025.3469 128966.4724
2929 2930
189244.9270 215842.7162 When applied to a fitted linear model, the predict function will automatically provide predicted values (\(\hat{y}\)) for the data originally used to fit the model. These training or in-sample predictions are somewhat useful and, if we had a second data set, we could use the newdata argument to get similar ‘test set’ or ‘out-of-sample’ predictions which would provide us a more nuanced view of model accuracy.
If we want to work with this model in more detail, the broom package provides useful functionality for tidyverse-type manipulation:
# A tibble: 1 × 12
r.squared adj.r.squared sigma statistic p.value df logLik AIC BIC
<dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 0.601 0.601 50475. 1103. 0 4 -35885. 71781. 71817.
# ℹ 3 more variables: deviance <dbl>, df.residual <int>, nobs <int>Here, we see that the glance function provides the usual ‘model-level’ statistics that can be used to assess how effective the model is. Perhaps the most important ones here are the r.squared value, indicating we capture about 60% of variability with this model, and the sigma value indicating that our predictions are typically off by about $50,000.
The tidy function gives us information about specific coefficients:
tidy(ames_lm)# A tibble: 5 × 5
term estimate std.error statistic p.value
<chr> <dbl> <dbl> <dbl> <dbl>
1 (Intercept) -60041. 4451. -13.5 2.77e- 40
2 Lot_Area 0.0975 0.127 0.770 4.41e- 1
3 First_Flr_SF 144. 2.66 54.2 0
4 Second_Flr_SF 82.9 2.27 36.5 6.97e-241
5 Central_AirY 48346. 3782. 12.8 1.93e- 36Probably the most useful column here is the estimate column, which provides the estimated regression coefficients.
We will have much more to say about these types of manipulations in class.
Not the average difference as this data has no paired structure.↩︎
You should be a bit unsatisfied with “enough” and “not too terrible”: these terms have more precise definitions, but they aren’t in our scope here.↩︎
The t_test function is a thin wrapper around the t.test function provided to us by base R. The infer version has the nice property of returning its results in a data frame, rather than a more obscure object type, but the specific values returned are equal, so it’s fine to use t.test instead.↩︎
On most US keyboards, the ~ character can be found just above the tab key on the right hand side, and can be typed by holding down shift and hitting the ` key.↩︎
You may have heard these variables referred to as the independent and dependent variables in other contexts. This terminology is absurd. In statistics, dependence is a symmetric relationship: \(Y\) depends on \(X\), then \(X\) depends on \(Y\); and if \(Y\) is independent of \(X\), then \(X\) is independent of \(Y\). Almost all of our methods are looking for some relationship between two variables, so a priori calling one of them “independent” is just silly.↩︎
It’s conventional to specify the alternative instead of the null, but if you recall your introductory courses, we really only test against the null, never for the alternative so I find this to be a strange design choice.↩︎
The specifics of mapping a categorical variable to a numerical model like linear regression are beyond what we talk about in this course, but surprisingly non-trivial. Ask your regression professor about contrasts or encodings.↩︎